Kvantna logična vrata
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 14:36, 15 maj 2008 (spremeni) Asistent (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (09:00, 23 maj 2008) (spremeni) (undo) Asistent (Pogovor | prispevki) |
||
| (One intermediate revision not shown.) | |||
| Vrstica 6: | Vrstica 6: | ||
| :<math>CNOT=\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}</math> (deluje v Hilbertovem prostoru dveh spinov 1/2) | :<math>CNOT=\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}</math> (deluje v Hilbertovem prostoru dveh spinov 1/2) | ||
| # Pokaži, kako lahko s temi operatorji tvorimo Bellova stanja. | # Pokaži, kako lahko s temi operatorji tvorimo Bellova stanja. | ||
| - | # Pokaži, kako lahko te operatorje | + | # Pokaži, da lahko te operatorje konstruiramo z vklapljanjem magnetnega polja, interakcije med spini in konstantnega potenciala v primerno dolgih časovnih intervalih. |
| - | + | == [[Media:kaučič.pdf|Rešitev]] == | |
| - | == Rešitev == | + | |
Trenutna redakcija
[spremeni] Naloga
V kvantem računalništvu naletimo na naslednja kvantna vrata, ki jih opišemo z operatorji
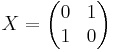(deluje v Hilbertovem prostoru spina 1/2)
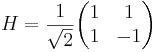(Hadamardova vrata, deluje v Hilbertovem prostoru spina 1/2)
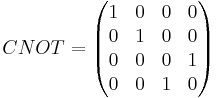(deluje v Hilbertovem prostoru dveh spinov 1/2)
- Pokaži, kako lahko s temi operatorji tvorimo Bellova stanja.
- Pokaži, da lahko te operatorje konstruiramo z vklapljanjem magnetnega polja, interakcije med spini in konstantnega potenciala v primerno dolgih časovnih intervalih.