Vrtilna količina II
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 11:42, 17 april 2008 (spremeni) Asistent (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (15:15, 6 maj 2008) (spremeni) (undo) Asistent (Pogovor | prispevki) |
||
| Vrstica 4: | Vrstica 4: | ||
| *Delec z vrtilno količino l = 1, ki se giblje v krogelno simetričnem potencialu, je v stanju m = 1. Ob t = 0 vklopimo homogeno magnetno polje v ravnini xz pod kotom <math>\varphi</math> glede na os z. Ob času <math>\pi/\omega_L</math> (<math>\omega_L</math> je Larmorjeva frekvenca) izmerimo projekcijo vrtilne količine delca na os z. Kolikšna je pričakovana vrednost meritve? S kolikšno verjetnostjo dobimo katerega od možnih rezultatov meritve? | *Delec z vrtilno količino l = 1, ki se giblje v krogelno simetričnem potencialu, je v stanju m = 1. Ob t = 0 vklopimo homogeno magnetno polje v ravnini xz pod kotom <math>\varphi</math> glede na os z. Ob času <math>\pi/\omega_L</math> (<math>\omega_L</math> je Larmorjeva frekvenca) izmerimo projekcijo vrtilne količine delca na os z. Kolikšna je pričakovana vrednost meritve? S kolikšno verjetnostjo dobimo katerega od možnih rezultatov meritve? | ||
| - | == Rešitev == | + | == [[Media:Podergajs.pdf|Rešitev]] == |
Trenutna redakcija
[spremeni] Naloga
- Zapiši operator, ki transformira valovno funkcijo v podprostoru l = 1 iz baze lastnih funkcij operatorja Lz v bazo lastnih funkcij operatorja
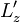 , kjer je kot med osema z in
, kjer je kot med osema z in 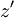 enak
enak 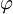 .
.
- Delec z vrtilno količino l = 1, ki se giblje v krogelno simetričnem potencialu, je v stanju m = 1. Ob t = 0 vklopimo homogeno magnetno polje v ravnini xz pod kotom
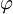 glede na os z. Ob času π / ωL (ωL je Larmorjeva frekvenca) izmerimo projekcijo vrtilne količine delca na os z. Kolikšna je pričakovana vrednost meritve? S kolikšno verjetnostjo dobimo katerega od možnih rezultatov meritve?
glede na os z. Ob času π / ωL (ωL je Larmorjeva frekvenca) izmerimo projekcijo vrtilne količine delca na os z. Kolikšna je pričakovana vrednost meritve? S kolikšno verjetnostjo dobimo katerega od možnih rezultatov meritve?