Vrtilna količina I
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 11:46, 16 april 2007 (spremeni) WikiSysop (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (11:37, 22 maj 2007) (spremeni) (undo) WikiSysop (Pogovor | prispevki) |
||
| (One intermediate revision not shown.) | |||
| Vrstica 1: | Vrstica 1: | ||
| + | == Naloga == | ||
| + | |||
| Delec je v stanju z valovno funkcijo <math>\psi({\mathbf r})=A(x+2 y+i z)e^{-\alpha r}</math>, kjer je <math>r=\sqrt{x^2+y^2+z^2}</math>. | Delec je v stanju z valovno funkcijo <math>\psi({\mathbf r})=A(x+2 y+i z)e^{-\alpha r}</math>, kjer je <math>r=\sqrt{x^2+y^2+z^2}</math>. | ||
| # Izračunaj pričakovano vrednost operatorjev <math>{\mathbf L}^2</math>, <math>L_x</math>, <math>L_y</math> in <math>L_z</math>. | # Izračunaj pričakovano vrednost operatorjev <math>{\mathbf L}^2</math>, <math>L_x</math>, <math>L_y</math> in <math>L_z</math>. | ||
| # Kolikšna je verjetnost, da pri meritvi <math>L_z</math> izmerimo vrednost <math>\hbar</math>? | # Kolikšna je verjetnost, da pri meritvi <math>L_z</math> izmerimo vrednost <math>\hbar</math>? | ||
| + | |||
| + | == [[Media:Petric.pdf|Rešitev]] == | ||
Trenutna redakcija
[spremeni] Naloga
Delec je v stanju z valovno funkcijo 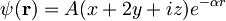 , kjer je
, kjer je 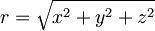 .
.
- Izračunaj pričakovano vrednost operatorjev
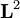 , Lx, Ly in Lz.
, Lx, Ly in Lz.
- Kolikšna je verjetnost, da pri meritvi Lz izmerimo vrednost
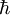 ?
?