Časovno odvisna perturbacija IV
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 17:51, 1 junij 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == Obravnavaj enodimenzionalni harmonski oscilator s hamiltonianom <math>H=\frac{p^2}{2m}+\frac{m\omega^2(t)x^2}{2}</math>, kjer je <math>\omega(t)=\omega_0+\delta\omega\cos...) ← Pojdi na prejšnje urejanje |
Redakcija: 13:21, 9 september 2007 (spremeni) (undo) Lautar (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 11: | Vrstica 11: | ||
| in <math>\delta\omega\ll\omega_0</math>. Ob <math>t=0</math> je sistem v osnovnem stanju. V prvem redu perturbacije poišči verjetnosti, da se ob času <math>t</math> sistem nahaja v <math>n</math>-tem vzbujenem stanju. | in <math>\delta\omega\ll\omega_0</math>. Ob <math>t=0</math> je sistem v osnovnem stanju. V prvem redu perturbacije poišči verjetnosti, da se ob času <math>t</math> sistem nahaja v <math>n</math>-tem vzbujenem stanju. | ||
| - | == Rešitev == | + | == [[Media:DomacaNaloga.pdf|Rešitev]] == |
Redakcija: 13:21, 9 september 2007
Naloga
Obravnavaj enodimenzionalni harmonski oscilator s hamiltonianom
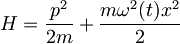 ,
,
kjer je
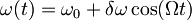
in 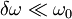 . Ob t = 0 je sistem v osnovnem stanju. V prvem redu perturbacije poišči verjetnosti, da se ob času t sistem nahaja v n-tem vzbujenem stanju.
. Ob t = 0 je sistem v osnovnem stanju. V prvem redu perturbacije poišči verjetnosti, da se ob času t sistem nahaja v n-tem vzbujenem stanju.