6. Skalarni produkt in korelacija

Iz Računalniška orodja v fiziki 2008 - 2009

V fiziki naletimo na pojem skalarnega produkta v dveh poglavitnih povezavah. Prva je skalarni produkt vektorjev 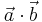$\vec{a}\cdot\vec{b}$ , ki se s komponentami vektorjev zapiše kot

skalab := 0; for i := 1 to 3 do skalab := skalab + a[i]*b[i]

Postopek se razširi na končnodimenzionalne vektorje iz linearne algebre preprosto tako, da poženemo zanko od 1 do n, kjer je n število dimenzij.

Druga povezava, v kateri naletimo na skalarni produkt, so funkcijski prostori. V Hilbertovem prostoru, ki je prostor funkcij $f (x)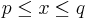$ , $p\leq x\leq q$ , za katere obstaja integral

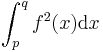$\int_p^q f^2(x)\mathrm{d}x$ ,

je skalarni produkt vektorjev/funkcij $a (x)$ in $b (x)$ definiran kot

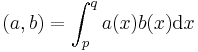$(a,b) = \int_p^q a(x)b(x) \mathrm{d}x$ .

Naj si predstavljamo stolpca a[i] in b[i] v tabeli podatkov kot n-razsežna vektorja ali kot funkciji, ki sta tabelirani v enakomernih razmikih, obakrat pridemo do enakega recepta za skalarni produkt, namreč tistega v prvi vrstici. Kvečjemu bi v primeru funkcij dobljeni rezultat skalab pomnožili še s h, z velikostjo koraka v tabeli. Za neenakomerno tabelo bi skalarni produkt uvedli po vzorcu, ki smo ga uporabili pri integriranju (5. tema).

Skalarni produkt meri projekcijo enega vektorja na drugega. V harmonski analizi razstavimo signal $a (x)$ v sinusne sestavine, tako da poiščemo skalarni produkt signala s sinusi in kosinusi različnih valovnih dolžin:

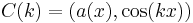$C(k) = \left(a(x), \cos(kx)\right)$ ,
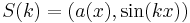$S(k) = \left(a(x), \sin(kx)\right)$ .

Funkcije $C (k)$ in $S (k)$ in še bolje, njuna pitagorejska vsota 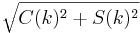$\sqrt{C(k)^2+S(k)^2}$ , imajo ekstrem pri tistih periodah $2π / k$ , ki so tudi periode signala.

Skalarni produkt dveh stolpcev podatkov $(a, b)$ meri tudi korelacijo teh dveh količin, kadar ju razumemo kot statistični (naključni) spremenljivki. Če vpeljemo povprečno vrednost produkta

r(a,b) = skalab/n

in jo še primerno premaknemo in normiramo

R(a,b) = (r(a,b) – apov*bpov)/(sigmaa*sigmab)

smo dobili brezdimenzijski korelacijski koeficient, ki lahko zavzame vrednosti med -1 in 1. Pozitivne vrednosti pomenijo, da sta spremenljivki korelirani, se pravi, da ena količina v povprečju raste, ko raste druga. Negativne vrednosti R pomenijo antikorelacijo, ko vrednosti prve količine v povprečju padajo, ko druge naraščajo. Pri tem so vrednosti na obeh konceh intervala rezervirane za jasne linearne odvisnosti količin; tiste v sredi, recimo med -0.3 in 0.3, pa za blago, komaj razločno povezavo med gibanjem obeh spremenljivk.

Pomembna karakteristika povezave signalov $a$ in $b$ je njuna korelacijska funkcija

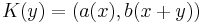$K(y) = \left(a(x), b(x+y)\right)$ ,

torej skalarni produkt pri zakasnitvi $y$ . Iz nje zelo jasno razberemo morebitne fazne premike signalov: zgodi se, da je skalarni produkt signalov majhen, da pa zrase, ko enega od signalov premaknemo po osi $x$ . Izračunamo jo lahko za vrednosti $y$ od - $n$ do $n$ . Seveda postaja z večanjem premika $y$ interval, po katerem lahko računamo skalarni produkt, vse krajši, zato je definicijo smiselno popraviti tako, da računamo povprečno vrednost produkta – se pravi, da pri vsakem $y$ delimo rezultat s številom točk, na katerih se signala sploh še prekrivata.

Tako funkcijo je zanimivo izračunati celo za en sam signal, takrat jo imenujemo avtokorelacijska funkcija:

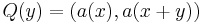$Q(y) = \left(a(x), a(x+y)\right)$ .

Pri periodičnih signalih lahko iz ekstremov $Q$ zelo natančno odčitamo periodo signala, pri neperiodičnih pa zvemo, kako daleč se signal "spominja" prejšnjega poteka.

V Mathematici skalarni produkt vektorjev a in b izračunamo z ukazom a.b, korelacijski koeficient med njima z ukazom Correlation, izračun korelacijske funkcije pa omogoča ukaz ListCorrelate.

Naloge:

V najnovejši številki Obzornika je objavljen zanimiv članek o miniaturni magnetni črpalki.^[1] Avtorji napovedo linearno zvezo med frekvenco rotorja in hitrostjo toka; meritve v datoteki "HitrostTokaOdFrekvence.txt" to potrjujejo. Določi korelacijski koeficient zveze med obema količinama.
Ameriška uprava za zdravila (FDA – Food and Drug Administration) je preskusila čudežno zdravilo mirabilitin za zvonjenje v ušesih (tintinabulus). V datoteki "Tintin.dat" so podani rezultati dvojno slepega preskusa. Določi korelacijski koeficient med dozo (v mg/kg žive mase) in stanjem bolezni po terapiji (ur zvonjenja na teden).
Pred leti smo v okviru mednarodnega projekta v našem znanem gradbenem podjetju merili hitrost strjevanja betona. Ulili so nekaj metrov velik betonski blok, v katerega je bila vdelana cela vrsta termočlenov za sprotno merjenje temperature. Datoteka "Beton.dat" podaja izmerke v razdobju šestih dni v dveh merilnih točkah. Prva je blizu površine, druga globoko v notranjosti. (Prvi stolpec je zaporedna številka meritve – časovni interval med njimi lahko oceniš iz očitnih dnevnih nihanj temperature.) Določi efektivno zakasnitev med obema signaloma iz njune korelacijske funkcije.
V datoteki "Luna.efe" je dana efemerida Lune za eno od preteklih let. Stolpci so: dan začenši s 1.1., nato rektascenzija (nebesna dolžina) v urah in minutah, in nazadnje deklinacija (nebesna širina) v stopinjah, ob 0^h svetovnega časa tega dne. Iz avtokorelacijske funkcije deklinacije čim bolj natančno določi Lunino periodo tira. (Lahko si pomagaš z odvajanjem.)

Literatura

↑ Blaž Kavčič, Dušan Babič in Igor Poberaj, Mikrofluidično vezje z mikročrpalko, OMF 56 (2009) 1.

[0] Blaž Kavčič, Dušan Babič in Igor Poberaj, Mikrofluidično vezje z mikročrpalko, OMF 56 (2009) 1.

[1]