5. Diferencialne operacije

Iz Računalniška orodja v fiziki 2008 - 2009

Količino, ki je definirana z odvodom merjene količine y, lahko določimo le približno, saj v tabeli ne moremo izpeljati limitnega procesa h→0, ki ga terja matematična definicija. Zadovoljimo se z diferenčnim približkom, v katerem je h kar korak naše tabele merjenih vrednosti:

for i:= t to n-1 do u[i] := (y[i+1]-y[i])/(x[i+1]-x[i]);

Vrednosti odvoda u[i] je v tem primeru treba pripisati vrednostim x na sredi intervala, torej smo pripravili novo tabelo parov u[i], xx[i] = (x[i+1]+x[i])/2, i:= 1, 2, ..., n-1. Kadar bi radi obdržali količini y in u v isti tabeli, torej pripisani istim x, je bolje uporabiti simetrično aproksimacijo za odvod, u[i] = (y[i+1]-y[i-1])/(x[i+1]-x[i-1]). Če se velikost koraka x v tabeli ne spreminja prehudo, lahko gornjo vrednost pripišemo abscisi x[i].

Odvajanje podatkov prinaša še eno neprijetnost, izgubo natančnosti. Pri količkaj gladki odvisnosti y(x) sta si sosednji vrednosti v tabeli blizu tudi po velikosti in je njuna razlika v števcu odvoda majhna. Njena natančnost (absolutna napaka) je istega reda velikosti kot napaka izmerkov – v resnici je za faktor √2 večja – zato pa je relativna napaka lahko dosti večja. Povedano drugače, napaka se začne na določeni decimalki merjenega rezultata. Ko dve taki vrednosti odštejemo, lahko izgubimo eno ali več vodilnih decimalk, tako da ima napaka v rezultatu odštevanja večji relativni delež. Zato so grafi odvodov vedno bolj zašumljeni (zobati) kot grafi izvirnih količin. Če se zanesemo na gladkost y, lahko zobatost odvoda popravimo z zglajenimi formulami, ki upoštevajo širši interval sosednjih vrednosti. – Ob povedanem je očitno, da potrebujemo za drugi odvod količine zelo natančne podatke, da se po dvakratnem odštevanju rezultat ne izgubi v šumu meritve.

Integracija, nasprotno, je stabilna operacija, ki ne ojačuje šuma meritve. Integralsko količino w[i] lahko dobimo s trapezno integracijo. Če je integrirana količina podana v ekvidistantni tabeli x[i] = x0 + i*h, i = 0, 1, 2, ..., n, dobimo integral od x0 do x[i]:

w[0] := 0; for i:= 1 to n do w[i] := w[i-1] + 0.5*h*(y[i-1] + y[i]).

V neenakomerni tabeli moramo namesto h vnesti "trenutno" velikost intervala x[i]-x[i-1]. Če nas ne moti, da je integrirana količina w podana v drugih točkah kot y, namreč v srednjih točkah intervalov, je mogoče zgornji račun še poenostaviti.

Naloge

Nariši graf diferencialne upornosti dU/dI za tokovno odvisnost v datoteki "Korozija.dat".
Za kovine je energija rentgenskega absorpcijskega robu definirana kot energija točke, v kateri ima absorpcijski spekter največjo strmino. Poišči to energijo za kovinski mangan iz spektra "Md29mn_00001.fio" (ln(I₂/I₃) iz naloge 4.3). Zadostuje, da določiš odvod v območju ~20 eV samega robu.
V matematiki se namesto naših porazdelitev, ki pomenijo gostoto verjetnosti, kadar jih pravilno normiramo na celotno število ali na celotno mero, dostikrat uporabljajo integralske verjetnosti, ki so definirane z integralom
$W(x) = \int_{-\infty}^x f(x)\mathrm{d}x$ ,
oziroma pač od spodnje meje porazdelitve. Določi $W (x)$ za podatke iz datoteke "Ozadje.dat" in iz histograma, dobljenega iz sinusne krivulje (naloga 2.4). Ali je iz slednjega rezultata mogoče uganiti analitični zapis porazdelitve?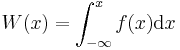