3. Povprečja

Iz Računalniška orodja v fiziki 2008 - 2009

Porazdelitev vrednosti spremenljivke je lahko zelo pestra in bogata, kot smo videli na naših zgledih. Kadar si hočemo to sliko poenostaviti na nekaj številskih parametrov, zelo pogosto uporabljamo povprečja. Povprečje spremenljivke same, ypov, je aritmetična sredina posameznih (izmerjenih) vrednosti:

sumy := 0;
for i := 1 to n do sumy := sumy + y[i];
ypov := sumy/n;

Če smo spremenljivko že opredalčkali v m predalčkov, je račun krajši:

for j := 1 to m do sumy := sumy + numy[j]*y[j]; 
ypov := sumy/n;

če pa smo register numy že normirali v nabor frekvenc f[j], pa celo

ypov := 0;
for j := 1 to m do ypov := ypov + f[j]*y[j].

y[j] označuje sredino intervala, ki ga zaseda j-ti predalček. Pri zvezno porazdeljenih spremenljivkah se utegneta prvotno in predalčno povprečje za malenkost razlikovati. Verjetnostna teorija zagotavlja, da razhajanje ni sistematično, ampak so predalčna povprečja (n.pr. za različne širine predalčkov) centrirana okoli pravega.

Podatek o srednji legi spremenljivke na osi količine y lahko obogatimo še z oceno o njeni razsutosti ali širini porazdelitve, sigmay. Imenujejo jo disperzija ali srednji kvadratni odmik.

sum2y := 0;
for i := 1 to n do sum2y := sum2y + sqr(y[i] – ypov); 
sigmay := sqrt(sum2y/n);

in analogno za opredalčene vrednosti. Pri tem je treba povedati, da je razhajanje med pravo in opredalčeno vrednostjo tu sistematično: razlika raste s kvadratom širine predalčkov in jo pri točnih računih upoštevajo.

Na prvi pogled se zdi, da terja izračun sigmay dva sprehoda skozi podatke: enega, da določimo ypov, in še enega za sigmay. V resnici je oboje mogoče opraviti z enim samim sprehodom, upoštevaje zvezo med obema spremenljivkama: vsota njunih kvadratov je enaka povprečju kvadrata spremenljivke. (To je trditev, katere vsebina je enaka Steinerjevemu stavku iz mehanike. Če si porazdelitev vrednosti spremenljivke predstavljamo kot porazdeljeno maso, določa ypov njeno težišče, sigmay pa njen vztrajnostni radij.)

sumy := 0;
sum2y := 0;
for i := 1 to n do begin
  sumy := sumy + y[i]; 
  sum2y := sum2y + sqr(y[i]) 
end;
ypov := sumy/n; 
sigmay := sqrt(sum2y/n – sqr(ypov));

Za spremenljivko, ki smo ji določili ypov in sigmay, si v najbolj grobem približku predstavljamo, da je porazdeljena po Gaussovi porazdelitvi

.

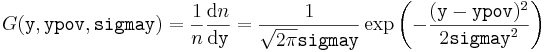Prvi popravek, poševnost muy, se izraža s povprečjem tretje potence

sum3y := 0;
for i := 1 to n do sum3y := sum3y + (y[i] – ypov)*sqr(y[i] – ypov);
muy := sum3y/(n*sigmay*sqr(sigmay));

Za račun povprečij so prikladna orodja preglednic, kot je Excel. Tudi v Mathematici lahko te količine enostavno izračunamo (glej poglavje tutorial/DescriptiveStatistics v pomoči), drugod pa je treba zapisati programsko vrstico. Za analizo numeričnih podatkov je zelo uporaben programski jezik Perl.

Naloge

1. Datoteka "Interval.dat" podaja časovne intervale (v mikrosekundah) med zaporednimi prihodi posameznih fotonov v detektor. Poišči povprečje ypov in sigmay za to zaporedje in za njegove tretjinske odseke.
2. Določi povprečja ypov, sigmay in muy za spremenljivki v podatkih "Agxx.dat" in "Ozadje.dat". Primerjaj direktna in predalčna povprečja. Nariši grafa za standardizirano spremenljivko u = (y – ypov)/sigmay. Primerjaj ju z grafom Gaussove porazdelitve G(u,0,1). Povprečje muy podaja (relativno) asimetrično odstopanje porazdelitve naše spremenljivke od G.
3. Določi povprečji ypov in sigmay za sinusno spremenljivko iz naloge 2.4. Po pričakovanju je ypov blizu 0. Ali lahko oceniš sigmay po analitični poti, z integralom po funkciji, ki definira spremenljivko? Poskusi najprej s približkom za celo število nihajev, nato pa še točneje v pravem intervalu naloge 2.4.