Časovno odvisna perturbacija IV

Iz Kvantna mehanika I 2007 - 2008

Revision as of 13:59, 14 maj 2008 by Krizaj (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Naloga

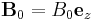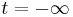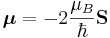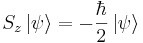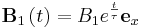Vodikov atom v homogenem magnetnem polju $\mathbf{B}_{0}=B_{0}\mathbf{e}_{z}$ je ob $t=-\infty$ v osnovnem stanju (ker je magnetni moment elektrona $\boldsymbol{\mu}=-2\frac{\mu_{B}}{\hbar}\mathbf{S}$ obrnjen nasprotno kot njegov spin, je v osnovnem stanju $S_{z}\left|\psi\right\rangle =-\frac{\hbar}{2}\left|\psi\right\rangle$ ). Nato vklopimo dodatno šibko magnetno polje $\mathbf{B}_{1}\left(t\right)=B_{1}e^{\frac{t}{\tau}}\mathbf{e}_{x}$ .

Kolikšna je verjetnost, da pri meritvi $S z$ ob $t = 0$ izmerimo vrednost 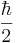$\frac{\hbar}{2}$ ? Računaj v prvem redu perturbacije!
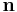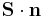
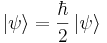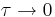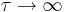V katero smer je ob $t = 0$ obrnjen elektronov spin (smer spina podaja enotski vektor $\mathbf{n}$ za katerega velja $\mathbf{S}\cdot\mathbf{n}$ $\left|\psi\right\rangle =\frac{\hbar}{2}\left|\psi\right\rangle$ ) v limitah $\tau\rightarrow0$ in $\tau\rightarrow\infty$ ? Pri katerem $τ$ pričakuješ prehod med obema režimoma?

Rešitev

Vzpostavljeno iz »http://burana.ijs.si/wiki5/index.php/%C4%8Casovno_odvisna_perturbacija_IV«