Kvantna logična vrata
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 14:28, 15 maj 2008 (spremeni) Asistent (Pogovor | prispevki) (New page: == Naloga == == Rešitev ==) ← Pojdi na prejšnje urejanje |
Redakcija: 14:36, 15 maj 2008 (spremeni) (undo) Asistent (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 1: | Vrstica 1: | ||
| == Naloga == | == Naloga == | ||
| + | |||
| + | V kvantem računalništvu naletimo na naslednja kvantna vrata, ki jih opišemo z operatorji | ||
| + | :<math>X=\begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix}</math> (deluje v Hilbertovem prostoru spina 1/2) | ||
| + | :<math>H=\frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1 \\ 1 & -1 \end{pmatrix}</math> (Hadamardova vrata, deluje v Hilbertovem prostoru spina 1/2) | ||
| + | :<math>CNOT=\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}</math> (deluje v Hilbertovem prostoru dveh spinov 1/2) | ||
| + | # Pokaži, kako lahko s temi operatorji tvorimo Bellova stanja. | ||
| + | # Pokaži, kako lahko te operatorje | ||
| + | |||
| == Rešitev == | == Rešitev == | ||
Redakcija: 14:36, 15 maj 2008
Naloga
V kvantem računalništvu naletimo na naslednja kvantna vrata, ki jih opišemo z operatorji
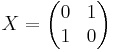 (deluje v Hilbertovem prostoru spina 1/2)
(deluje v Hilbertovem prostoru spina 1/2)
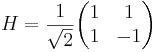 (Hadamardova vrata, deluje v Hilbertovem prostoru spina 1/2)
(Hadamardova vrata, deluje v Hilbertovem prostoru spina 1/2)
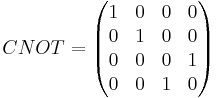 (deluje v Hilbertovem prostoru dveh spinov 1/2)
(deluje v Hilbertovem prostoru dveh spinov 1/2)
- Pokaži, kako lahko s temi operatorji tvorimo Bellova stanja.
- Pokaži, kako lahko te operatorje