Tridimenzionalni harmonski oscilator I
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 15:27, 7 maj 2008 (spremeni) Asistent (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Redakcija: 15:28, 7 maj 2008 (spremeni) (undo) Asistent (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 3: | Vrstica 3: | ||
| Obravnavaj lastna stanja izotropnega tridimenzionalnega harmonskega oscilatorja | Obravnavaj lastna stanja izotropnega tridimenzionalnega harmonskega oscilatorja | ||
| :<math>H=\frac{\mathbf{p^2}}{2m}+\frac{1}{2}a {\mathbf r}^2</math>. | :<math>H=\frac{\mathbf{p^2}}{2m}+\frac{1}{2}a {\mathbf r}^2</math>. | ||
| - | *Za prvo vzbujeno stanje poišči taka lastna stanja, ki so hkrati tudi lastna stanja operatorja vrtilne količine okoli osi <math>z</math>. | + | *Za prvo vzbujeno stanje poišči taka lastna stanja, ki so hkrati tudi lastna stanja operatorja vrtilne količine okoli osi <math>z</math> in kvadrata velikosti vrtilne količine. |
| *Kako se prvo vzbujeno stanje razcepi v homogenem magnetnem polju v smeri osi z? | *Kako se prvo vzbujeno stanje razcepi v homogenem magnetnem polju v smeri osi z? | ||
| == Rešitev == | == Rešitev == | ||
Redakcija: 15:28, 7 maj 2008
Naloga
Obravnavaj lastna stanja izotropnega tridimenzionalnega harmonskega oscilatorja
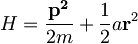 .
.
- Za prvo vzbujeno stanje poišči taka lastna stanja, ki so hkrati tudi lastna stanja operatorja vrtilne količine okoli osi z in kvadrata velikosti vrtilne količine.
- Kako se prvo vzbujeno stanje razcepi v homogenem magnetnem polju v smeri osi z?