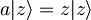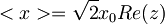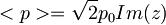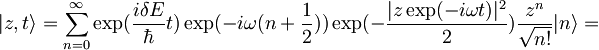Koherentna stanja harmonskega oscilatorja II
Iz Kvantna mehanika I 2007 - 2008
| Redakcija: 18:31, 20 marec 2008 (spremeni) 212.235.211.117 (Pogovor) ← Pojdi na prejšnje urejanje |
Redakcija: 17:25, 22 april 2008 (spremeni) (undo) 92.37.14.166 (Pogovor) Novejše urejanje → |
||
| Vrstica 4: | Vrstica 4: | ||
| == Rešitev == | == Rešitev == | ||
| + | |||
| + | S klasično mehaniko bi ta problem lahko predstavljal žogico, nabito z nabojem <math>e^+\,\!</math>, ki je pritrjena na vzmet s konstanto vzmeti <math>k\,\!</math>, v času <math>t=0\,\!</math> vključimo zunanje električno polje <math>\vec E\,\!</math>, ki kaže v smeri vzmeti. Žogica se potem odmakne za <math>\delta \vec x = \frac{e\vec E}{k}</math> in tam obmiruje, tako da je pričakovana vrednost položaja delca v klasičnem primeru <math>\delta \vec x = \frac{e\vec E}{k}</math>, pričakovana vrednost gibalne količine <math>\vec p=0\,\!</math> in pričakovana vrednost energije <math>W=\frac{k\delta x^2}{2}</math>, pričakovane vrednosti se s časom ne spreminjajo. | ||
| + | |||
| + | ==Reševanje v kvantni mehaniki== | ||
| + | |||
| + | Stanja oscilatorja(nabitega delca) bodo za čase <math>t<0</math>, opisovale količine brez vijuge, za čase <math>t\ge 0</math> pa količine z vijugo. | ||
| + | |||
| + | <math>t<0\,\!</math>: | ||
| + | |||
| + | <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math> | ||
| + | |||
| + | <math>t\ge 0</math>: | ||
| + | |||
| + | <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}+e\phi(x)</math> | ||
| + | |||
| + | <math>\vec E=-\nabla\phi(x)</math>, ker je <math>\vec E =konst=-\nabla\phi(x)</math> in je <math> \vec E =(E_x,0,0) </math> je <math>\phi(x)=-E_xx\,\!</math> <math>\Rightarrow H=\frac {p^2}{2m}+\frac{kx^2}{2}-eEx </math> Člen <math>\frac{kx^2}{2}-eEx</math> bom zapisal kot | ||
| + | <math>\frac{kx^2}{2}-eEx=\frac{k}{2}(x-\frac{eE}{k})^2-\frac{e^2E^2}{2k}</math> in ga še polepšam z novima oznakama <math>\delta x=\frac{eE}{k}</math> in <math>\delta E=\frac{e^2E^2}{2k}</math> da dobim: <math>\frac{kx^2}{2}-eEx=\frac{k}{2}(x-\delta x)^2-\delta E</math> | ||
| + | |||
| + | Povezava med <math>x\,\!</math> '''''in''''' <math>\tilde{x}\,\!</math>: | ||
| + | |||
| + | <math>\tilde{x}=x-\delta x</math> -za novo izhodišče koordinatnega sistema po vklopu polja sem izbral novo mirovno lego delca, ki je prvotne legepremaknjena za <math>\delta x\,\!</math> v desno. | ||
| + | |||
| + | <math>\tilde{p}=-i\hbar\frac{\partial}{\partial \tilde{x}}=-i\hbar\frac{\partial}{\partial (x-\delta x)}=-i\hbar\frac{\partial}{\partial x} \Rightarrow \tilde{p}=p</math>, operator gibalne količine se ne spremeni! | ||
| + | |||
| + | Z novimi koordinatami se hamilton zapiše: | ||
| + | |||
| + | <math>\tilde{H}=\frac{\tilde{p}^2}{2m}+\frac{k\tilde{x}^2}{2}-\delta E=\frac{p^2}{2m}+\frac{k\tilde{x}^2}{2}-\delta E</math> | ||
| + | ---- | ||
| + | <math>H=\hbar\omega(a^\dagger a+\frac{1}{2})</math> | ||
| + | |||
| + | <math>\tilde{H}=\hbar\tilde{\omega}(\tilde{a}^\dagger \tilde{a}+\frac{1}{2})-\delta E</math> | ||
| + | |||
| + | Ker se frekvenca po vklopu polja ne spremeni je <math>\tilde{\omega}=\omega</math> zato je <math>\tilde{H}=\hbar\omega(\tilde{a}^\dagger\tilde{a}+\frac{1}{2})-\delta E</math> | ||
| + | |||
| + | Povezava med <math>a\,\!</math> in <math>\tilde{a}\,\!</math>: | ||
| + | |||
| + | <math>a=\frac{1}{\sqrt{2}}(\frac{x}{x_0}+i\frac{p}{p_0})</math> | ||
| + | |||
| + | <math>\tilde{a}=\frac{1}{\sqrt{2}}(\frac{\tilde{x}}{x_0}+i\frac{\tilde{p}}{p_0})=\frac{1}{\sqrt{2}}(\frac{x-\delta x}{x_0}+i\frac{p}{p_0})=a-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0} \Rightarrow \tilde{a}=a-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0}</math> | ||
| + | ---- | ||
| + | Na začetku: <math>a|\psi\rangle=0</math>, delec je v osnovnem stanju starega <math>H\,\!</math>. | ||
| + | |||
| + | <math>0=a|\psi(0)\rangle=(\tilde{a}+\frac{1}{\sqrt{2}}\frac{\delta x}{x_0})|\psi(0)\rangle \Rightarrow \tilde{a}|\psi(0)\rangle=-\frac{1}{sqrt{2}}\frac{\delta x}{x_0}|\psi(0)\rangle \Rightarrow \text{staro stanje je koherentno stanje novega hamiltona }\tilde{a}\psi(0)=z\psi(0) \text{; }</math> | ||
| + | |||
| + | <math>z=-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0}</math> | ||
| + | |||
| + | Za koherentna stanja <math>z\,\!</math> velja: | ||
| + | |||
| + | #<math>a|z\rangle=z|z\rangle</math> | ||
| + | #<math><x>=\sqrt{2}x_0Re(z)</math> | ||
| + | #<math><p>=\sqrt{2}p_0Im(z)</math> | ||
| + | |||
| + | Za našo nalogo bom potreboval prejšnje tri lastnosti, ampak za časovno odvisna koherentna stanja, tako da jih bom še malo predelal: | ||
| + | |||
| + | <math>|z\rangle=\sum_{n=0}^{\infty}\exp(-\frac{|z|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle\,\!</math> -razvoj koherenčnega stanja po lastnih funkcijah hamiltonovega operatorja | ||
| + | |||
| + | <math>|z,t\rangle=\sum_{n=0}^{\infty}\exp(-\frac{iE_n}{\hbar}t)\exp(-\frac{|z|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle\,\!</math> -za časovni razvoj samo dodamo člen <math>\exp(-\frac{iE_n}{\hbar}t)\,\!</math>, <math>E_n\,\!</math> je v naši nalogi <math>\hbar\omega(n+\frac{1}{2})-\delta E\,\!</math> | ||
| + | |||
| + | <math>|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-i\omega(n+\frac{1}{2}))\exp(-\frac{|z|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle</math> | ||
| + | |||
| + | Ker je <math>|\exp(-i\omega t)|=1\,\!</math> in je zato <math>|z|=|z||\exp(-i\omega t)|=|z\exp(-i\omega t)|\,\!</math>, bom v zgornjo enačbo za <math>z\,\!</math> vstavil <math>|z|=|z\exp(-i\omega t)|\,\!</math>: | ||
| + | |||
| + | <math>|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-i\omega(n+\frac{1}{2}))\exp(-\frac{|z\exp(-i\omega t)|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle=</math> | ||
| + | |||
| + | <math>=|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})\exp\left(-\frac{|z\exp(-i\omega t)|^2}{2}\right)\frac{(z\exp(-i\omega t))^n}{\sqrt{n!}}|n\rangle</math> | ||
| + | |||
| + | Konstanto <math>\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})</math> bom označil z <math>A\,\!</math> in <math>z\exp(-i\omega t)\,\!</math> z <math>u\,\!</math>.Tako je: | ||
| + | <math>|z,t\rangle=\sum_{n=0}{\infty}A\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle\,\!</math> | ||
| + | |||
| + | Vemo, da velja <math>\tilde{a}|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle= u|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math>, ker je <math>\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math> razvoj koherentnega stanja za <math>\tilde{a}\,\!</math> po lastnih funkcijah hamiltonovega operatorja. | ||
| + | |||
| + | To upoštevam v našem primeru: | ||
| + | |||
| + | <math>|z,t\rangle=\sum_{n=0}^{\infty}A\exp\left(-\frac{|u|^2}{2}\right)\frac{u^n}{\sqrt{n!}}|n\rangle</math> in | ||
| + | <math>\tilde{a}|z,t\rangle=\tilde{a}|\sum_{n=0}^{\infty}A\exp\left(-\frac{|u|^2}{2}\right)\frac{u^n}{\sqrt{n!}}|n\rangle= | ||
| + | u|\sum_{n=0}^{\infty}A\exp\left(-\frac{|u|^2}{2}\right)\frac{u^n}{\sqrt{n!}}|n\rangle \Rightarrow u=z\exp(-i\omega t)</math> je koherentna vrednost za | ||
| + | <math>|z,t\rangle</math>, nazaj pogledam vrednost za z: <math>z=-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0}\,\!</math>, potem je <math>u=-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0}\exp(-i\omega t)</math> | ||
| + | |||
| + | Pričakovana vrednost položaja: | ||
| + | |||
| + | <math><\tilde{x}>=\sqrt{2}x_0Re(u)=\sqrt{2}x_0(-\frac{1}{\sqrt{2}}\frac{\delta x}{x_0}\cos(\omega t))=-\delta x\cos(\omega t)</math> in | ||
| + | <math><x>=\delta x(1-\cos(\omega t))\,\!</math> | ||
| + | |||
| + | Pričakovana vrednost gibalne količine: | ||
| + | |||
| + | Ehrenfestov teorem: <math><p>=m<\dot x></math> | ||
| + | |||
| + | <math><p>=m<\dot x>=m\sin(\omega t)</math> -izračunana z ehrenfestovim teoremom. | ||
| + | |||
| + | Iz lastnosti koherentnih stanj: <math><p>=\sqrt{2}p_0Im(u)=\sqrt{2}p_0(\frac{\delta x}{\sqrt{2}x_0}\sin(\omega t))=\frac{\sqrt{2}\hbar\delta x}{\sqrt{2}x_0^2}\sin(\omega t)=m\omega\delta x\sin(\omega t)</math> -upošteval sem, da je <math>p_0=\frac{\hbar}{x_0}</math> in | ||
| + | <math>x_0=\sqrt{\frac{\hbar}{m\omega}}</math> torej je <math><p>=m\omega\delta x | ||
| + | \sin \omega t\,\!</math>, kar je isto kot rezultat izračunan z ehrenfestovim teoremom. | ||
Redakcija: 17:25, 22 april 2008
Naloga
Delec z nabojem e je v osnovnem stanju harmonskega oscilatorja 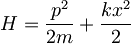 . Ob t = 0 v trenutku vključimo homogeno električno polje E. Kako se s časom spreminjajo pričakovane vrednosti položaja, gibalne količine in energije delca?
. Ob t = 0 v trenutku vključimo homogeno električno polje E. Kako se s časom spreminjajo pričakovane vrednosti položaja, gibalne količine in energije delca?
Rešitev
S klasično mehaniko bi ta problem lahko predstavljal žogico, nabito z nabojem 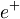 , ki je pritrjena na vzmet s konstanto vzmeti
, ki je pritrjena na vzmet s konstanto vzmeti 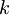 , v času
, v času 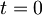 vključimo zunanje električno polje
vključimo zunanje električno polje 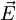 , ki kaže v smeri vzmeti. Žogica se potem odmakne za
, ki kaže v smeri vzmeti. Žogica se potem odmakne za 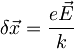 in tam obmiruje, tako da je pričakovana vrednost položaja delca v klasičnem primeru
in tam obmiruje, tako da je pričakovana vrednost položaja delca v klasičnem primeru 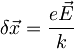 , pričakovana vrednost gibalne količine
, pričakovana vrednost gibalne količine 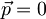 in pričakovana vrednost energije
in pričakovana vrednost energije 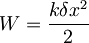 , pričakovane vrednosti se s časom ne spreminjajo.
, pričakovane vrednosti se s časom ne spreminjajo.
Reševanje v kvantni mehaniki
Stanja oscilatorja(nabitega delca) bodo za čase t < 0, opisovale količine brez vijuge, za čase 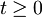 pa količine z vijugo.
pa količine z vijugo.
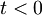 :
:
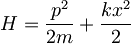
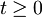 :
:
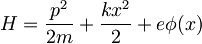
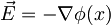 , ker je
, ker je 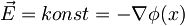 in je
in je 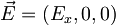 je
je 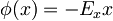
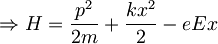 Člen
Člen 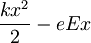 bom zapisal kot
bom zapisal kot
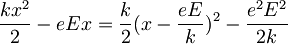 in ga še polepšam z novima oznakama
in ga še polepšam z novima oznakama 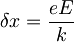 in
in 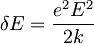 da dobim:
da dobim: 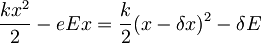
Povezava med 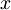 in
in 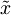 :
:
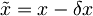 -za novo izhodišče koordinatnega sistema po vklopu polja sem izbral novo mirovno lego delca, ki je prvotne legepremaknjena za
-za novo izhodišče koordinatnega sistema po vklopu polja sem izbral novo mirovno lego delca, ki je prvotne legepremaknjena za 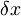 v desno.
v desno.
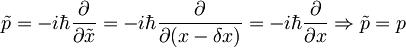 , operator gibalne količine se ne spremeni!
, operator gibalne količine se ne spremeni!
Z novimi koordinatami se hamilton zapiše:
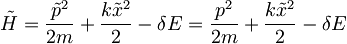
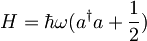
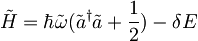
Ker se frekvenca po vklopu polja ne spremeni je 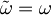 zato je
zato je 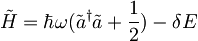
Povezava med 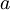 in
in 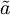 :
:
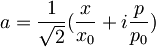
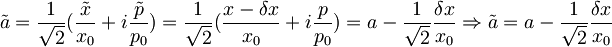
Na začetku: 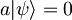 , delec je v osnovnem stanju starega
, delec je v osnovnem stanju starega  .
.
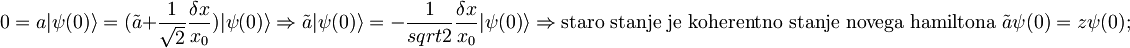
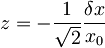
Za koherentna stanja  velja:
velja:
Za našo nalogo bom potreboval prejšnje tri lastnosti, ampak za časovno odvisna koherentna stanja, tako da jih bom še malo predelal:
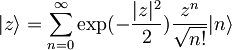 -razvoj koherenčnega stanja po lastnih funkcijah hamiltonovega operatorja
-razvoj koherenčnega stanja po lastnih funkcijah hamiltonovega operatorja
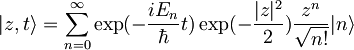 -za časovni razvoj samo dodamo člen
-za časovni razvoj samo dodamo člen 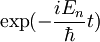 ,
, 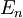 je v naši nalogi
je v naši nalogi 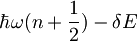
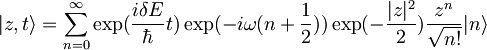
Ker je 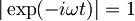 in je zato
in je zato 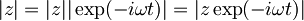 , bom v zgornjo enačbo za
, bom v zgornjo enačbo za  vstavil
vstavil 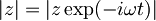 :
:
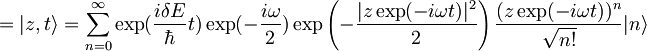
Konstanto 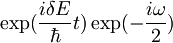 bom označil z
bom označil z 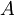 in
in 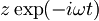 z
z 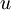 .Tako je:
.Tako je:
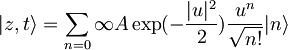
Vemo, da velja 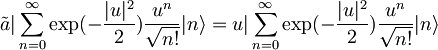 , ker je
, ker je 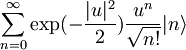 razvoj koherentnega stanja za
razvoj koherentnega stanja za 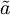 po lastnih funkcijah hamiltonovega operatorja.
po lastnih funkcijah hamiltonovega operatorja.
To upoštevam v našem primeru:
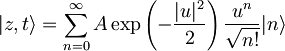 in
in
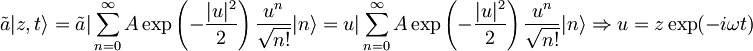 je koherentna vrednost za
je koherentna vrednost za
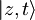 , nazaj pogledam vrednost za z:
, nazaj pogledam vrednost za z: 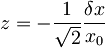 , potem je
, potem je 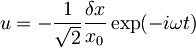
Pričakovana vrednost položaja:
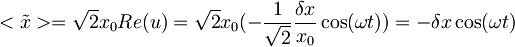 in
in
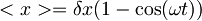
Pričakovana vrednost gibalne količine:
Ehrenfestov teorem: 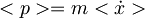
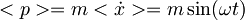 -izračunana z ehrenfestovim teoremom.
-izračunana z ehrenfestovim teoremom.
Iz lastnosti koherentnih stanj: 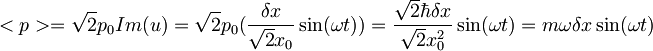 -upošteval sem, da je
-upošteval sem, da je 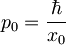 in
in
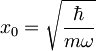 torej je
torej je 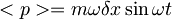 , kar je isto kot rezultat izračunan z ehrenfestovim teoremom.
, kar je isto kot rezultat izračunan z ehrenfestovim teoremom.