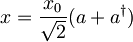Harmonski oscilator
Iz Kvantna mehanika I 2007 - 2008
| Redakcija: 14:29, 20 marec 2008 (spremeni) Asistent (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Redakcija: 11:19, 25 marec 2008 (spremeni) (undo) Asistent (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 5: | Vrstica 5: | ||
| == Rešitev == | == Rešitev == | ||
| + | |||
| + | Hamiltonovo funkcijo za harmonski oscilator lahko namesto z operatorjema lege in gibalne količine izrazimo kot funkcijo anihilacijskega ter kreacijskega (ki je kar adjungirani anihilacijski operator) operatorja | ||
| + | :<math>H = \hbar \omega (a^{\dagger}a + \frac{1}{2})</math>, | ||
| + | pri čemer je <math>\omega = \sqrt{\frac{k}{m}}</math> , anihalicijski operator pa je enak | ||
| + | :<math>a = \frac{1}{\sqrt 2} (\frac{x}{x_0} + i \frac{p}{p_0})</math> , | ||
| + | pri čemer je <math>x_0 = \sqrt{\frac{\hbar}{m \omega}}</math>, <math>p_0 = \frac{\hbar}{x_0}</math> . | ||
| + | |||
| + | Lastnim funkcijam oz. stanjem harmonskega oscilatorja (<math>\left|0\right\rangle</math> , <math>\left| 1\right\rangle</math>, <math>\left|2\right\rangle</math>, ....) ustrezajo določene diskretne vrednosti energije <math>E_n</math>, ki predstavljajo lastne vrednosti Hamiltonovega operatorja | ||
| + | :<math>H \left| n\right\rangle = E_n \left| n\right\rangle</math> . | ||
| + | |||
| + | Vrednosti teh energij določa enačba | ||
| + | :<math>E_n = \hbar \omega (n + \frac{1}{2})</math> . | ||
| + | |||
| + | Kako anihalicijski ter kreacijski operator delujeta na lastne funkcije podajajo naslednje zvaze: | ||
| + | *<math>a\left| 0\right\rangle = 0</math> | ||
| + | *<math>a\left| n\right\rangle = \sqrt n \left| n-1\right\rangle</math> | ||
| + | *<math>a^{\dagger}\left| 0\right\rangle = 1</math> | ||
| + | *<math>a^{\dagger}\left| n\right\rangle = \sqrt {n+1} \left| | ||
| + | n+1\right\rangle</math> . | ||
| + | |||
| + | Časovni razvoj dane valovne funkcije je enak: | ||
| + | :<math>|\psi,t\rangle = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{E_{0}}{\hbar}t} + |1\rangle e^{-i\frac{E_{1}}{\hbar}t} \right) = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{\omega}{2}t} + |1\rangle e^{-i\frac{3\omega}{2}t} \right) </math> . | ||
| + | Iz definicij anihilacijskega ter lreacijskega operatorja izrazimo operator lege | ||
| + | :<math>x = \frac{x_0}{\sqrt 2} (a + a^{\dagger})</math> | ||
| + | in uporabimo pri izračunu časovne odvisnosti pričakovane lege | ||
| + | :<math>\langle x(t) \rangle = \langle \psi | x \psi \rangle =\frac{x_0}{\sqrt 2} (\langle a \rangle + \langle a^{\dagger} \rangle) =\frac{x_0}{\sqrt 2} 2 Re(\langle a \rangle) = \sqrt 2 x_0 Re(\langle a\rangle)</math> . | ||
Redakcija: 11:19, 25 marec 2008
Naloga
- Kako se s časom spreminjata pričakovani vrednosti operatorjev x in x2 v stanju
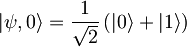 harmonskega oscilatorja
harmonskega oscilatorja 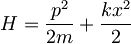 ?
?
- S pomočjo anihilacijskega in kreacijskega operatorja določi valovni funkciji osnovnega in prvega vzbujenega stanja harmonskega oscilatorja v koordinatni reprezentaciji.
Rešitev
Hamiltonovo funkcijo za harmonski oscilator lahko namesto z operatorjema lege in gibalne količine izrazimo kot funkcijo anihilacijskega ter kreacijskega (ki je kar adjungirani anihilacijski operator) operatorja
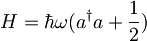 ,
,
pri čemer je 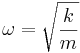 , anihalicijski operator pa je enak
, anihalicijski operator pa je enak
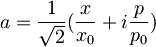 ,
,
pri čemer je 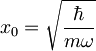 ,
, 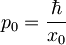 .
.
Lastnim funkcijam oz. stanjem harmonskega oscilatorja (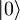 ,
, 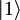 ,
, 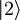 , ....) ustrezajo določene diskretne vrednosti energije En, ki predstavljajo lastne vrednosti Hamiltonovega operatorja
, ....) ustrezajo določene diskretne vrednosti energije En, ki predstavljajo lastne vrednosti Hamiltonovega operatorja
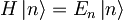 .
.
Vrednosti teh energij določa enačba
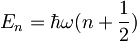 .
.
Kako anihalicijski ter kreacijski operator delujeta na lastne funkcije podajajo naslednje zvaze:
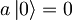
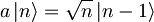
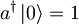
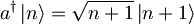 .
.
Časovni razvoj dane valovne funkcije je enak:
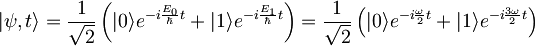 .
.
Iz definicij anihilacijskega ter lreacijskega operatorja izrazimo operator lege
in uporabimo pri izračunu časovne odvisnosti pričakovane lege
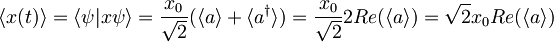 .
.