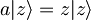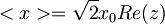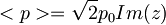Koherentna stanja harmonskega oscilatorja II
Iz Kvantna mehanika I 2007 - 2008
| Redakcija: 18:21, 22 april 2008 (spremeni) 92.37.7.15 (Pogovor) ← Pojdi na prejšnje urejanje |
Redakcija: 11:04, 23 april 2008 (spremeni) (undo) 193.2.4.4 (Pogovor) Novejše urejanje → |
||
| Vrstica 66: | Vrstica 66: | ||
| Ker je <math>|\exp(-i\omega t)|=1\,\!</math> in je zato <math>|z|=|z||\exp(-i\omega t)|=|z\exp(-i\omega t)|\,\!</math>, bom v zgornjo enačbo za <math>z\,\!</math> vstavil <math>|z|=|z\exp(-i\omega t)|\,\!</math>: | Ker je <math>|\exp(-i\omega t)|=1\,\!</math> in je zato <math>|z|=|z||\exp(-i\omega t)|=|z\exp(-i\omega t)|\,\!</math>, bom v zgornjo enačbo za <math>z\,\!</math> vstavil <math>|z|=|z\exp(-i\omega t)|\,\!</math>: | ||
| - | <math>|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-i\omega(n+\frac{1}{2}))\exp(-\frac{|z\exp(-i\omega t)|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle=</math> | + | <math>|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-i\omega(n+\frac{1}{2}))\exp(-\frac{|z\exp(-i\omega t)|^2}{2})\frac{z^n}{\sqrt{n!}}|n\rangle=</math> |
| <math>=|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})\exp\left(-\frac{|z\exp(-i\omega t)|^2}{2}\right)\frac{(z\exp(-i\omega t))^n}{\sqrt{n!}}|n\rangle</math> | <math>=|z,t\rangle=\sum_{n=0}^{\infty}\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})\exp\left(-\frac{|z\exp(-i\omega t)|^2}{2}\right)\frac{(z\exp(-i\omega t))^n}{\sqrt{n!}}|n\rangle</math> | ||
| Konstanto <math>\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})</math> bom označil z <math>A\,\!</math> in <math>z\exp(-i\omega t)\,\!</math> z <math>u\,\!</math>.Tako je: | Konstanto <math>\exp(\frac{i\delta E}{\hbar}t)\exp(-\frac{i\omega}{2})</math> bom označil z <math>A\,\!</math> in <math>z\exp(-i\omega t)\,\!</math> z <math>u\,\!</math>.Tako je: | ||
| - | <math>|z,t\rangle=\sum_{n=0}{\infty}A\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle\,\!</math> | + | <math>|z,t\rangle=\sum_{n=0}^{\infty}A\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle\,\!</math> |
| Vemo, da velja <math>\tilde{a}|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle= u|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math>, ker je <math>\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math> razvoj koherentnega stanja za <math>\tilde{a}\,\!</math> po lastnih funkcijah hamiltonovega operatorja. | Vemo, da velja <math>\tilde{a}|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle= u|\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math>, ker je <math>\sum_{n=0}^\infty\exp(-\frac{|u|^2}{2})\frac{u^n}{\sqrt{n!}}|n\rangle</math> razvoj koherentnega stanja za <math>\tilde{a}\,\!</math> po lastnih funkcijah hamiltonovega operatorja. | ||
Redakcija: 11:04, 23 april 2008
Naloga
Delec z nabojem e je v osnovnem stanju harmonskega oscilatorja 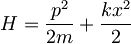 . Ob t = 0 v trenutku vključimo homogeno električno polje E. Kako se s časom spreminjajo pričakovane vrednosti položaja, gibalne količine in energije delca?
. Ob t = 0 v trenutku vključimo homogeno električno polje E. Kako se s časom spreminjajo pričakovane vrednosti položaja, gibalne količine in energije delca?
Rešitev
S klasično mehaniko bi ta problem lahko predstavljal žogico, nabito z nabojem 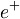 , ki je pritrjena na vzmet s konstanto vzmeti
, ki je pritrjena na vzmet s konstanto vzmeti 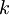 , v času
, v času 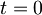 vključimo zunanje električno polje
vključimo zunanje električno polje 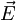 , ki kaže v smeri vzmeti. Žogica se potem odmakne za
, ki kaže v smeri vzmeti. Žogica se potem odmakne za 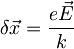 in tam obmiruje, tako da je pričakovana vrednost položaja delca v klasičnem primeru
in tam obmiruje, tako da je pričakovana vrednost položaja delca v klasičnem primeru 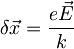 , pričakovana vrednost gibalne količine
, pričakovana vrednost gibalne količine 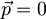 in pričakovana vrednost energije
in pričakovana vrednost energije 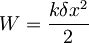 , pričakovane vrednosti se s časom ne spreminjajo.
, pričakovane vrednosti se s časom ne spreminjajo.
Reševanje v kvantni mehaniki
Stanja oscilatorja(nabitega delca) bodo za čase t < 0, opisovale količine brez vijuge, za čase 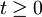 pa količine z vijugo.
pa količine z vijugo.
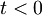 :
:
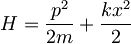
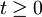 :
:
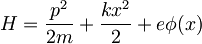
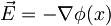 , ker je
, ker je 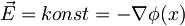 in je
in je 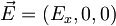 je
je 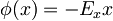
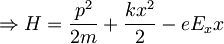 Člen
Člen 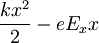 bom zapisal kot
bom zapisal kot
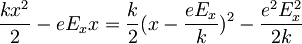 in ga še polepšam z novima oznakama
in ga še polepšam z novima oznakama 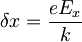 in
in 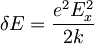 da dobim:
da dobim: 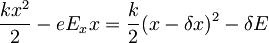
Povezava med 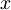 in
in 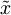 :
:
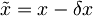 -za novo izhodišče koordinatnega sistema po vklopu polja sem izbral novo mirovno lego delca, ki je prvotne legepremaknjena za
-za novo izhodišče koordinatnega sistema po vklopu polja sem izbral novo mirovno lego delca, ki je prvotne legepremaknjena za 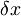 v desno.
v desno.
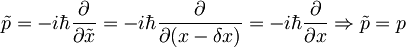 , operator gibalne količine se ne spremeni!
, operator gibalne količine se ne spremeni!
Z novimi koordinatami se hamilton zapiše:
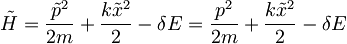
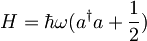
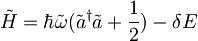
Ker se frekvenca po vklopu polja ne spremeni je 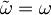 zato je
zato je 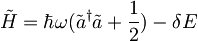
Povezava med 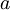 in
in 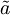 :
:
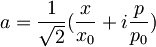
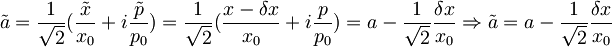
Na začetku: 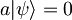 , delec je v osnovnem stanju starega
, delec je v osnovnem stanju starega  .
.

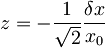
Za koherentna stanja 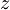 velja:
velja:
Za našo nalogo bom potreboval prejšnje tri lastnosti, ampak za časovno odvisna koherentna stanja, tako da jih bom še malo predelal:
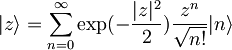 -razvoj koherenčnega stanja po lastnih funkcijah hamiltonovega operatorja
-razvoj koherenčnega stanja po lastnih funkcijah hamiltonovega operatorja
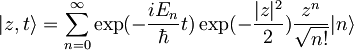 -za časovni razvoj samo dodamo člen
-za časovni razvoj samo dodamo člen 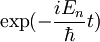 ,
, 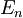 je v naši nalogi
je v naši nalogi 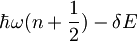
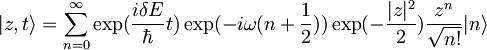
Ker je 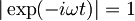 in je zato
in je zato 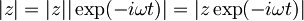 , bom v zgornjo enačbo za
, bom v zgornjo enačbo za 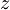 vstavil
vstavil 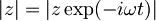 :
:
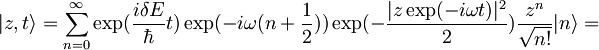
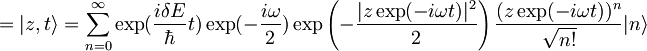
Konstanto 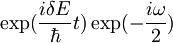 bom označil z
bom označil z 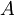 in
in 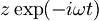 z
z 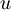 .Tako je:
.Tako je:
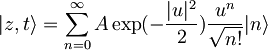
Vemo, da velja 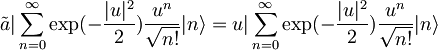 , ker je
, ker je 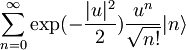 razvoj koherentnega stanja za
razvoj koherentnega stanja za 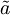 po lastnih funkcijah hamiltonovega operatorja.
po lastnih funkcijah hamiltonovega operatorja.
To upoštevam v našem primeru:
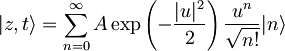 in
in
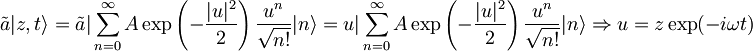 je koherentna vrednost za
je koherentna vrednost za
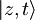 , nazaj pogledam vrednost za z:
, nazaj pogledam vrednost za z: 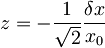 , potem je
, potem je 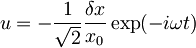
Pričakovana vrednost položaja:
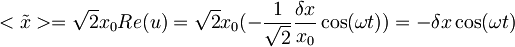 in
in
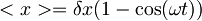
Pričakovana vrednost gibalne količine:
Ehrenfestov teorem: 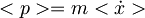
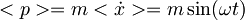 -izračunana z ehrenfestovim teoremom.
-izračunana z ehrenfestovim teoremom.
Iz lastnosti koherentnih stanj: 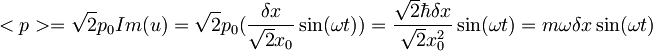 -upošteval sem, da je
-upošteval sem, da je 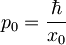 in
in
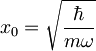 torej je
torej je 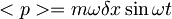 , kar je isto kot rezultat izračunan z ehrenfestovim teoremom.
, kar je isto kot rezultat izračunan z ehrenfestovim teoremom.