Koherentna stanja harmonskega oscilatorja I
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 18:27, 20 marec 2008 (spremeni) 212.235.211.117 (Pogovor) (New page: == Naloga == Za delec v koherentnem stanju <math>a\left|z\right\rangle=z\left|z\right\rangle</math> harmonskega oscilatorja <math>H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right)</math> ...) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (22:12, 14 maj 2008) (spremeni) (undo) 212.235.211.117 (Pogovor) |
||
| ( not shown.) | |||
| Vrstica 1: | Vrstica 1: | ||
| == Naloga == | == Naloga == | ||
| - | Za delec v koherentnem stanju <math>a\left|z\right\rangle=z\left|z\right\rangle</math> harmonskega oscilatorja <math>H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right)</math> izračunaj nedoločenosti položaja in gibalne količine. Zapiši valovno funkcijo koherentnega stanja v koordinatni reprezentaciji. | + | Za delec v koherentnem stanju <math>a\left|z\right\rangle=z\left|z\right\rangle</math> harmonskega oscilatorja <math>H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right)</math> |
| + | # izračnuja časovni razvoj valovne funkcije, | ||
| + | # izračunaj nedoločenosti položaja in gibalne količine delca, | ||
| + | # zapiši valovno funkcijo v koordinatni reprezentaciji. | ||
| - | == Rešitev == | + | == [[Media:Dergan.pdf|Rešitev]]== |
Trenutna redakcija
[spremeni] Naloga
Za delec v koherentnem stanju 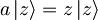 harmonskega oscilatorja
harmonskega oscilatorja 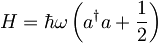
- izračnuja časovni razvoj valovne funkcije,
- izračunaj nedoločenosti položaja in gibalne količine delca,
- zapiši valovno funkcijo v koordinatni reprezentaciji.