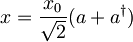Harmonski oscilator
Iz Kvantna mehanika I 2007 - 2008
| Redakcija: 14:29, 20 marec 2008 (spremeni) Asistent (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (11:47, 25 julij 2008) (spremeni) (undo) 89.142.56.30 (Pogovor) (pravopis) |
||
| ( not shown.) | |||
| Vrstica 5: | Vrstica 5: | ||
| == Rešitev == | == Rešitev == | ||
| + | |||
| + | Hamiltonovo funkcijo za harmonski oscilator lahko namesto z operatorjema lege in gibalne količine izrazimo kot funkcijo anihilacijskega ter kreacijskega (ki je kar adjungirani anihilacijski operator) operatorja | ||
| + | :<math>H = \hbar \omega (a^{\dagger}a + \frac{1}{2})</math>, | ||
| + | pri čemer je <math>\omega = \sqrt{\frac{k}{m}}</math> , anihalicijski operator pa je enak | ||
| + | :<math>a = \frac{1}{\sqrt 2} (\frac{x}{x_0} + i \frac{p}{p_0})</math> , | ||
| + | pri čemer je <math>x_0 = \sqrt{\frac{\hbar}{m \omega}}</math>, <math>p_0 = \frac{\hbar}{x_0}</math> . | ||
| + | |||
| + | Lastnim funkcijam oz. stanjem harmonskega oscilatorja (<math>\left|0\right\rangle</math> , <math>\left| 1\right\rangle</math>, <math>\left|2\right\rangle</math>, ....) ustrezajo določene diskretne vrednosti energije <math>E_n</math>, ki predstavljajo lastne vrednosti Hamiltonovega operatorja | ||
| + | :<math>H \left| n\right\rangle = E_n \left| n\right\rangle</math> . | ||
| + | |||
| + | Vrednosti teh energij določa enačba | ||
| + | :<math>E_n = \hbar \omega (n + \frac{1}{2})</math> . | ||
| + | |||
| + | Kako anihalicijski ter kreacijski operator delujeta na lastne funkcije podajajo naslednje zveze: | ||
| + | *<math>a\left| 0\right\rangle = 0</math> | ||
| + | *<math>a\left| n\right\rangle = \sqrt n \left| n-1\right\rangle</math> | ||
| + | *<math>a^{\dagger}\left| 0\right\rangle = | 1\rangle</math> (na vajah smo narobe pisali le 1) | ||
| + | *<math>a^{\dagger}\left| n\right\rangle = \sqrt {n+1} \left| | ||
| + | n+1\right\rangle</math> . | ||
| + | |||
| + | Časovni razvoj dane valovne funkcije je enak: | ||
| + | :<math>|\psi,t\rangle = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{E_{0}}{\hbar}t} + |1\rangle e^{-i\frac{E_{1}}{\hbar}t} \right) = \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{\omega}{2}t} + |1\rangle e^{-i\frac{3\omega}{2}t} \right) </math> . | ||
| + | Iz definicij anihilacijskega ter kreacijskega operatorja izrazimo operator lege | ||
| + | :<math>x = \frac{x_0}{\sqrt 2} (a + a^{\dagger})</math> | ||
| + | in uporabimo pri izračunu časovne odvisnosti pričakovane lege | ||
| + | :<math>\langle x(t) \rangle = \langle \psi | x \psi \rangle =\frac{x_0}{\sqrt 2} (\langle a \rangle + \langle a^{\dagger} \rangle) =\frac{x_0}{\sqrt 2} 2 Re(\langle a \rangle) = \sqrt 2 x_0 Re(\langle a\rangle)</math> . | ||
| + | |||
| + | Tako je potrebno izračunati pričakovano vrednost anihilacijskega operatorja | ||
| + | :<math>\langle a \rangle = \langle \psi | a \psi \rangle = \frac{1}{\sqrt{2}}\left( \langle 0| e^{-i\frac{\omega}{2}t} + \langle 1| e^{-i\frac{3\omega}{2}t} \right) | a \frac{1}{\sqrt{2}}\left( |0\rangle e^{-i\frac{\omega}{2}t} + |1\rangle e^{-i\frac{3\omega}{2}t} \right)</math>. | ||
| + | |||
| + | Anihilacijski operator a deluje na funkcijo psi (desni oklepaj) po zgoraj navedenih pravilih | ||
| + | :<math>\langle a \rangle = \frac{1}{2} \left( \langle 0| e^{-i\frac{\omega}{2}t} + \langle 1| e^{-i\frac{3\omega}{2}t} \right) \left( 0 + \sqrt 1 |0\rangle e^{-i\frac{3\omega}{2}t}\right)</math> . | ||
| + | |||
| + | Nato se pri množenju upošteva ortogonalnost in normiranost lastnih funkcij | ||
| + | :<math>\langle a \rangle = \frac{1}{2}\left( e^{i\frac{\omega}{2}t - i\frac{3\omega}{2}t} + 0\right) = \frac{1}{2} e^{-i\omega t}</math> . | ||
| + | |||
| + | To vstavimo v izraz za pričakovano vrednost lege in upoštevamo, da je realni del eksponenta kosinus in dobimo | ||
| + | :<math>\langle x(t) \rangle = \frac{x_0 \sqrt 2}{2} \cos{\omega t}</math> . | ||
| + | |||
| + | Podobno izračunamo pričakovano vrednost kvadrata lege: | ||
| + | :<math>\langle x(t)^2 \rangle = \langle \psi | x^2 \psi \rangle = \langle \frac{x_0^2}{2}(a + a^{\dagger})^2\rangle = \frac{x_0^2}{2} \langle (a + a^{\dagger})^2\rangle = \frac{x_0^2}{2} (\langle a a\rangle + \langle a a^{\dagger}\rangle + \langle a^{\dagger} a\rangle + \langle a^{\dagger} a^{\dagger}\rangle)</math> . | ||
| + | |||
| + | Nato preoblikujemo izraz v | ||
| + | :<math>\langle x(t)^2 \rangle = \frac{x_0^2}{2} (2 Re(\langle a^2\rangle ) + \langle 2 a a^{\dagger}\rangle - 1)</math> , | ||
| + | pri čemer uporabimo dejstvo, da je komutator anihilacijskega ter kreacijskega operatorja enak 1 | ||
| + | :<math>\left[ a,a^{\dagger} \right] = aa^{\dagger} - a^{\dagger}a = 1</math> . | ||
| + | |||
| + | Podobno kot <math>\langle a\rangle</math> poračunamo tudi <math>\langle a^2\rangle</math>, to je dvakrat delujemo z opeatorjem a na funkcijo <math>\psi</math>, kar da po zgoraj zapisanih formulah rezultat 0. | ||
| + | |||
| + | Tako je potrebno poračunati le še | ||
| + | :<math>\langle a a^{\dagger}\rangle = \langle \psi | a a^{\dagger} \psi \rangle = \langle a^{\dagger}\psi | a^{\dagger} \psi \rangle</math> , | ||
| + | kjer je bra enak ketu, le da ima kompleksno konjugirane koeficiente. Kot za operator <math>a</math> poračunamo | ||
| + | :<math>| a^{\dagger} \psi \rangle = \frac{1}{\sqrt 2} (\sqrt{0+1}|0+1\rangle e^{-i\frac{\omega}{2}t} + \sqrt{1+1} | 1+1 \rangle e^{-i3\frac{\omega}{2}t}) = \frac{1}{\sqrt 2} (|1\rangle e^{-i\frac{\omega}{2}t} + \sqrt{2} | 2 \rangle e^{-i3\frac{\omega}{2}t})</math> . | ||
| + | |||
| + | Tako dobimo: | ||
| + | :<math>\langle a^{\dagger}\psi | a^{\dagger} \psi \rangle = \frac{1}{\sqrt 2} \frac{1}{\sqrt 2} (\langle 1|e^{i\frac{\omega}{2}t} + \sqrt 2 \langle 2 | e^{i3\frac{\omega}{2}t})(|1\rangle e^{-i\frac{\omega}{2}t} + \sqrt{2} | 2 \rangle e^{-i3\frac{\omega}{2}t}) = \frac{1}{2}(\langle 1|1\rangle e^0 +0 + 0 + 2\langle2|2\rangle e^0) = \frac{3}{2}</math> , | ||
| + | pri čemer smo zopet upoštevali ortonormiranost lastnih funkcij. | ||
| + | |||
| + | Pričakovana vrednost kvadrata odmika je tako | ||
| + | :<math>\langle x(t)^2 \rangle = \frac{x_0^2}{2}(2\frac{3}{2} - 1) = x_0^2</math> . | ||
| + | |||
| + | <hr> | ||
| + | |||
| + | Diracov zapis <math>a|0\rangle = 0</math> prevedemo v koordinatni zapis | ||
| + | :<math>\frac{1}{\sqrt 2}(\frac{x}{x_0} + i\frac{p}{p_0})\psi_0 (x) = 0</math> , | ||
| + | rešitev te diferencialne enačbe pa je | ||
| + | :<math>\psi (x) = \frac{1}{\sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}}</math> . | ||
| + | |||
| + | Podobno | ||
| + | :<math>a^{\dagger}|0\rangle = |1\rangle \Rightarrow \frac{1}{\sqrt 2}(\frac{x}{x_0} + i\frac{p}{p_0})\psi_0 (x) = \psi_1 (x) = \frac{1}{\sqrt 2}(\frac{x}{x_0} - \frac{\hbar}{p_0} \frac{\partial}{\partial x})\psi_0 (x) = \frac{1}{\sqrt 2}(\frac{x}{x_0} - x_0 \frac{\partial}{\partial x})\psi_0 (x) =</math> | ||
| + | :<math>= \frac{x}{x_0 \sqrt{2} \sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}} - \frac{x_0}{\sqrt{2} \sqrt[4]{x_0^2 \pi}}\left( - \frac{2 x}{x_0^2}\right) e^{- \frac{x^2}{2x_0^2}} = \frac{1}{\sqrt{2} \sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}}(\frac{x}{x_0} + \frac{x}{x_0})</math> . | ||
| + | |||
| + | Rezultat: | ||
| + | :<math>\psi_1 (x) = \sqrt 2 \frac{x}{x_0} \psi_0</math> . | ||
Trenutna redakcija
[spremeni] Naloga
- Kako se s časom spreminjata pričakovani vrednosti operatorjev x in x2 v stanju
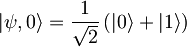 harmonskega oscilatorja
harmonskega oscilatorja 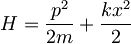 ?
?
- S pomočjo anihilacijskega in kreacijskega operatorja določi valovni funkciji osnovnega in prvega vzbujenega stanja harmonskega oscilatorja v koordinatni reprezentaciji.
[spremeni] Rešitev
Hamiltonovo funkcijo za harmonski oscilator lahko namesto z operatorjema lege in gibalne količine izrazimo kot funkcijo anihilacijskega ter kreacijskega (ki je kar adjungirani anihilacijski operator) operatorja
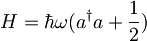 ,
,
pri čemer je 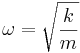 , anihalicijski operator pa je enak
, anihalicijski operator pa je enak
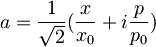 ,
,
pri čemer je 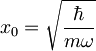 ,
, 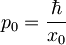 .
.
Lastnim funkcijam oz. stanjem harmonskega oscilatorja (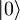 ,
, 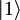 ,
, 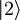 , ....) ustrezajo določene diskretne vrednosti energije En, ki predstavljajo lastne vrednosti Hamiltonovega operatorja
, ....) ustrezajo določene diskretne vrednosti energije En, ki predstavljajo lastne vrednosti Hamiltonovega operatorja
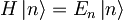 .
.
Vrednosti teh energij določa enačba
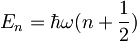 .
.
Kako anihalicijski ter kreacijski operator delujeta na lastne funkcije podajajo naslednje zveze:
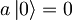
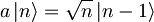
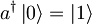 (na vajah smo narobe pisali le 1)
(na vajah smo narobe pisali le 1)
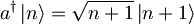 .
.
Časovni razvoj dane valovne funkcije je enak:
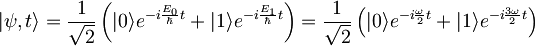 .
.
Iz definicij anihilacijskega ter kreacijskega operatorja izrazimo operator lege
in uporabimo pri izračunu časovne odvisnosti pričakovane lege
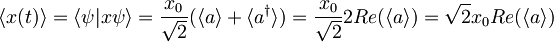 .
.
Tako je potrebno izračunati pričakovano vrednost anihilacijskega operatorja
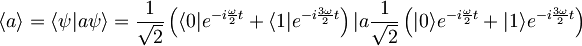 .
.
Anihilacijski operator a deluje na funkcijo psi (desni oklepaj) po zgoraj navedenih pravilih
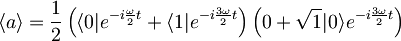 .
.
Nato se pri množenju upošteva ortogonalnost in normiranost lastnih funkcij
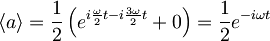 .
.
To vstavimo v izraz za pričakovano vrednost lege in upoštevamo, da je realni del eksponenta kosinus in dobimo
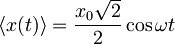 .
.
Podobno izračunamo pričakovano vrednost kvadrata lege:
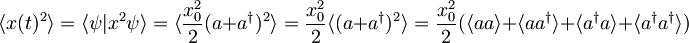 .
.
Nato preoblikujemo izraz v
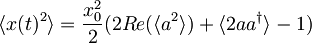 ,
,
pri čemer uporabimo dejstvo, da je komutator anihilacijskega ter kreacijskega operatorja enak 1
![\left[ a,a^{\dagger} \right] = aa^{\dagger} - a^{\dagger}a = 1](/wiki5/images/math/7/7/d/77d4f5aa941c7139f7399174a7e13931.png) .
.
Podobno kot 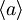 poračunamo tudi
poračunamo tudi 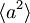 , to je dvakrat delujemo z opeatorjem a na funkcijo ψ, kar da po zgoraj zapisanih formulah rezultat 0.
, to je dvakrat delujemo z opeatorjem a na funkcijo ψ, kar da po zgoraj zapisanih formulah rezultat 0.
Tako je potrebno poračunati le še
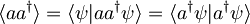 ,
,
kjer je bra enak ketu, le da ima kompleksno konjugirane koeficiente. Kot za operator a poračunamo
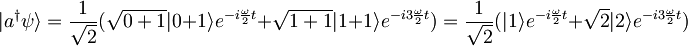 .
.
Tako dobimo:
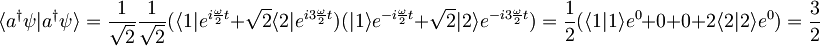 ,
,
pri čemer smo zopet upoštevali ortonormiranost lastnih funkcij.
Pričakovana vrednost kvadrata odmika je tako
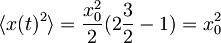 .
.
Diracov zapis 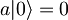 prevedemo v koordinatni zapis
prevedemo v koordinatni zapis
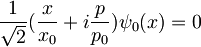 ,
,
rešitev te diferencialne enačbe pa je
![\psi (x) = \frac{1}{\sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}}](/wiki5/images/math/f/6/7/f67ee8c49720aa60945fc52325c2c1cf.png) .
.
Podobno
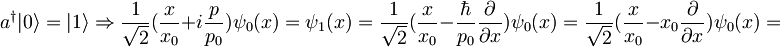
![= \frac{x}{x_0 \sqrt{2} \sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}} - \frac{x_0}{\sqrt{2} \sqrt[4]{x_0^2 \pi}}\left( - \frac{2 x}{x_0^2}\right) e^{- \frac{x^2}{2x_0^2}} = \frac{1}{\sqrt{2} \sqrt[4]{x_0^2 \pi}}e^{- \frac{x^2}{2x_0^2}}(\frac{x}{x_0} + \frac{x}{x_0})](/wiki5/images/math/0/5/0/0509f2867bbe92697fa9769faf3f6a46.png) .
.
Rezultat:
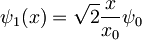 .
.