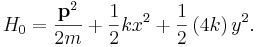Degenerirana perturbacija VIII
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 12:44, 8 maj 2008 (spremeni) Asistent (Pogovor | prispevki) (New page: == Naloga == Obravnavaj dvodimenzionalni harmonski oscilator :<math>H_{0}=\frac{\mathbf{p}^{2}}{2m}+\frac{1}{2}kx^{2}+\frac{1}{2}\left(4k\right)y^{2}.</math> #Kolikokrat je degeneriran en...) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (12:44, 8 maj 2008) (spremeni) (undo) Asistent (Pogovor | prispevki) |
||
| Vrstica 4: | Vrstica 4: | ||
| :<math>H_{0}=\frac{\mathbf{p}^{2}}{2m}+\frac{1}{2}kx^{2}+\frac{1}{2}\left(4k\right)y^{2}.</math> | :<math>H_{0}=\frac{\mathbf{p}^{2}}{2m}+\frac{1}{2}kx^{2}+\frac{1}{2}\left(4k\right)y^{2}.</math> | ||
| #Kolikokrat je degeneriran energijski nivo z energijo <math>\frac{11}{2}\hbar\omega</math>, kjer je <math>\omega=\sqrt{\frac{k}{m}}</math>? Zapiši bazo podprostora, ki ustreza temu energijskemu nivoju. | #Kolikokrat je degeneriran energijski nivo z energijo <math>\frac{11}{2}\hbar\omega</math>, kjer je <math>\omega=\sqrt{\frac{k}{m}}</math>? Zapiši bazo podprostora, ki ustreza temu energijskemu nivoju. | ||
| - | #Kaj se zgodi s stanji tega energijskega nivoja, če na delec poleg harmonskega potenciala deluje še anharmonska motnja | + | #Kaj se zgodi s stanji tega energijskega nivoja, če na delec poleg harmonskega potenciala deluje še anharmonska motnja <math>H=H_{0}+\lambda x^{2}y</math>? |
| - | :<math>H=H_{0}+\lambda x^{2}y</math>? | + | :Računaj v prvem redu perturbacije! |
| - | Računaj v prvem redu perturbacije! | + | |
| == Rešitev == | == Rešitev == | ||
Trenutna redakcija
[spremeni] Naloga
Obravnavaj dvodimenzionalni harmonski oscilator
- Kolikokrat je degeneriran energijski nivo z energijo
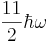, kjer je 
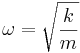? Zapiši bazo podprostora, ki ustreza temu energijskemu nivoju.
- Kaj se zgodi s stanji tega energijskega nivoja, če na delec poleg harmonskega potenciala deluje še anharmonska motnja H = H0 + λx2y?
- Računaj v prvem redu perturbacije!