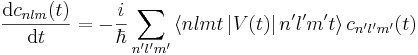Časovno odvisna perturbacija V

Iz Kvantna mehanika I 2007 - 2008

[spremeni] Naloga

Vodikov atom je v homogenem električnem polju

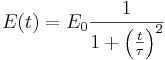$E(t)=E_0\frac{1}{1+\left(\frac{t}{\tau}\right)^2}$ .

Kolikšna je verjetnost, daje atom ob 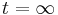$t=\infty$ v prvem vzbujenem stanju, če je bil ob 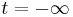$t=-\infty$ v osnovnem stanju? Pri katerem $τ$ je ta verjetnost največja? Predpostavi, da je električno polje dovolj šibko, da lahko uporabiš perturbacijsko teorijo.

[spremeni] Rešitev

Nika je opazila, da smo na vajah napačno zapisali formulo za popravek v prvem redu časovno odvisne perturbacije. Enačba (4) v poročilu bi se morala glasiti

$\frac{\mathrm{d}c_{nlm}(t)}{\mathrm{d}t}=-\frac{i}{\hbar}\sum_{n^\prime l^\prime m^\prime}\left\langle nlmt\left|V(t)\right|n^\prime l^\prime m^\prime t\right\rangle c_{n^\prime l^\prime m^\prime}(t)$

Posledično so napačne tudi enačbe (5) - (11), končni rezultat pa je pravilen. Kot vajo za kolokvij bi predlagal, da sami popravite še ostale napačne enačbe. Lp Tomaž

Vzpostavljeno iz »http://burana.ijs.si/wiki5/index.php/%C4%8Casovno_odvisna_perturbacija_V«