Kronig-Penneyev model kristala

Iz Fizika trdne snovi 2007 - 2008

Revision as of 23:22, 19 januar 2008 by 213.250.63.205 (Pogovor)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

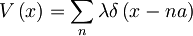
Imamo delec v 1D Kronig-Penneyevem potencialu: $V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)$

Iščemo lastne funkcije energije za ta sistem.

Potencial je več kot očitno periodičen: 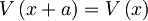$V\left(x+a\right)=V\left(x\right)$

Torej tudi za Hamiltonov operator: 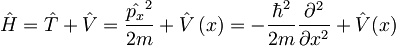$\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)$ velja, da je periodičen: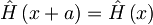 $\hat{H}\left(x+a\right)=\hat{H}\left(x\right)$

Uvedimo operator translacije: 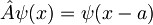$\hat{A}\psi(x)=\psi(x-a)$

Za lastne funkcije tega operatorja torej sledi: 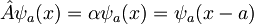$\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)$

Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza: 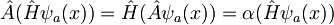$\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))$ .

Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: 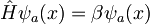$\hat{H}\psi_a(x)=\beta\psi_a(x)$

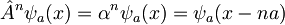
Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na. $\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)$

Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: $| α | = 1$ , torej jo lahko zapišemo kot $α = e - i φ$ oziroma, če to izrazimo s periodo a, kot $α = e - i k a$

Če sedaj povzamemo vse skupaj: $ψ a (x - a) = e - i k a ψ a (x)$ , oziroma $ψ a (x) e i k a = ψ a (x + a)$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Kronig-Penneyev_model_kristala«