Kronig-Penneyev model kristala

Iz Fizika trdne snovi 2007 - 2008

(Primerjava redakcij)

Redakcija: 23:45, 21 januar 2008

Imamo delec v 1D Kronig-Penneyevem potencialu:

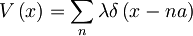
$V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)$

Iščemo lastne funkcije energije za ta sistem.

Potencial je več kot očitno periodičen: 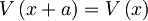$V\left(x+a\right)=V\left(x\right)$

Torej tudi za Hamiltonov operator velja, da je periodičen: 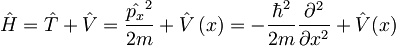$\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)$

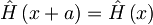
$\hat{H}\left(x+a\right)=\hat{H}\left(x\right)$

Uvedimo operator translacije: 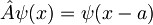$\hat{A}\psi(x)=\psi(x-a)$

Za lastne funkcije tega operatorja torej sledi: 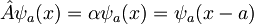$\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)$

Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza: 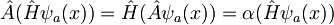$\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))$ .

Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: 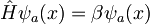$\hat{H}\psi_a(x)=\beta\psi_a(x)$

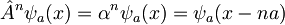
Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na. $\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)$

Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: $| α | = 1$ , torej jo lahko zapišemo kot $α = e - i φ$ oziroma, če to izrazimo s periodo a, kot $α = e - i k a$

Če sedaj povzamemo vse skupaj: $ψ a (x - a) = e - i k a ψ a (x)$ , oziroma $ψ a (x) e i k a = ψ a (x + a)$

Sedaj uporabimo sledeči nastavek: $ψ a (x) = e i k x u (x)$ , katerega nesemo v zgornjo enačbo: $e i k (x + a) u (x) = e i k (x + a) u (x + a)$ in od tod dobimo pogoj za funkcijo u(x): $u (x) = u (x + a)$ . Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala.

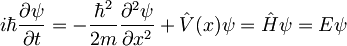
Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe: $i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi$

Rešitve v vmesnih področjih, kjer je V=0, so oblike

$ψ n (x) = A n e i q x + B n e - i q x = ψ n (x) = e i k x (A n e i (q - k) x + B n e - i (q + k) x) = e i k x u n (x)$ , kjer je $ψ n (x)$ lastna funkcija energije v n-tem področju in 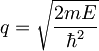$q= \sqrt{\frac{2mE}{\hbar^2}}$

Sedaj nesemo dobljeni izraz za u(x) v pogoj, dobljen iz periodičnosti potenciala: u(x)=u(x+a):

$u n (x) = u n + 1 (x + a)$

$A n e i (q - k) x + B n e - i (q + k) x = A n + 1 e i (q - k)(x + a) + B n + 1 e - i (q + k)(x + a)$

Ker to velja za vsak x, sledi:

$A n + 1 = A n e - i (q - k) a$

$B n + 1 = B n e i (q + k) a$ , torej

$A n = A e - i (q - k) n a$

$B n = B e i (q + k) n a$ , kjer sta: $A = A 0$ in $B = B 0$

Torej lahko zapišemo rešitev Schrodingerjeve enačbe za n-to področje kot:

$ψ n (x) = e i k x (A e i (q - k)(x - n a) + B e - i (q + k)(x - n a)) =$

$= A e i q x e - i (q - k) n a + B e - i q x e i (q + k) n a$

Neznane količine: q (in torej tudi lastne energije E), A in B, dobimo iz začetnih in robnih pogojev.

Robni pogoji:

1.) $ψ n - 1 (x = n a) = ψ n (x = n a)$

2.) 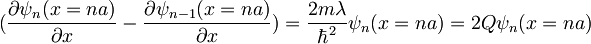$(\frac{\partial\psi_{n}(x=na)}{\partial{x}}-\frac{\partial\psi_{n-1}(x=na)}{\partial{x}})=\frac{2m\lambda}{\hbar^2}\psi_{n}(x=na)=2Q\psi_{n}(x=na)$ , kjer je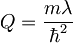 $Q=\frac{m\lambda}{\hbar^2}$

Ko vstavimo valovno funkcijo v prvi robni pogoj, dobimo:

$ψ n - 1 (n a) = ψ n (n a)$

$A n - 1 e i q n a + B n - 1 e - i q n a = A n - 1 e - i (q - k) a e i q n a + B n - 1 e i (q + k) a e - i q n a$

$A n - 1 e i q n a (1 - e - i q a e i k a) = B n - 1 e - i q n a (e i q a e i k a - 1)$

Iz drugega robnega pogoja pa dobimo:

$ψ n'(n a) - ψ n - 1'(n a) = 2 Q ψ n (n a)$

$i q (A n - 1 e - i (q - k) a e i q n a - B n - 1 e i (q + k) a e - i q n a - A n - 1 e i q n a + B n - 1 e - i q n a) = 2 Q (A n - 1 e - i (q - k) a e i q n a + B n - 1 e i (q + k) a e - i q n a)$

$A n - 1 e i q n a (i q e - i q a e i k a - i q - 2 Q e - i q a e i k a) = B n - 1 e - i q n a (i q e i q a e i k a - i q + 2 Q e i q a e i k a)$

Sedaj lahko med seboj zdelimo obe enačbi, ki sledita iz robnih pogojev, ter se tako znebimo konstant A in B

$(1 - e - i q a e i k a)(i q e i q a e i k a - i q + 2 Q e i q a e i k a) = (e i q a e i k a - 1)(i q e - i q a e i k a - i q - 2 Q e - i q a e i k a)$

$(i q e i q a e i k a - i q + 2 Q e i q a e i k a - i q e 2 i k a + i q e - i q a e i k a - 2 Q e 2 i k a) = (i q e 2 i k a - i q e i q a e i k a - 2 Q e 2 i k a - i q e - i q a e i k a + i q + 2 Q e - i q a e i k a)$

Pomnožimo celotno enačbo s členom $e - i k a$

$(i q e i q a - i q e - i k a + 2 Q e i q a - i q e i k a + i q e - i q a - 2 Q e i k a) = (i q e i k a - i q e i q a - 2 Q e i k a - i q e - i q a + i q e - i k a + 2 Q e - i q a)$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Kronig-Penneyev_model_kristala«

 <math>A_{n-1}e^{iqna}(1-e^{-iqa}e^{ika})=B_{n-1}e^{-iqna}(e^{iqa}e^{ika}-1)</math>
+Iz drugega robnega pogoja pa dobimo:
+<math>\psi_{n}'(na)-\psi_{n-1}'(na)=2Q\psi_{n}(na)</math>
+<math>iq(A_{n-1}e^{-i(q-k)a}e^{iqna}-B_{n-1}e^{i(q+k)a}e{-iqna}-A_{n-1}e^{iqna}+B_{n-1}e^{-iqna})=2Q(A_{n-1}e^{-i(q-k)a}e^{iqna}+B_{n-1}e^{i(q+k)a}e{-iqna})</math>
+<math>A_{n-1}e^{iqna}(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika})=B_{n-1}e^{-iqna}(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika})</math>
+Sedaj lahko med seboj zdelimo obe enačbi, ki sledita iz robnih pogojev, ter se tako znebimo konstant ''A'' in ''B''
+<math>(1-e^{-iqa}e^{ika})(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika})=(e^{iqa}e^{ika}-1)(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika})</math>
+<math>(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}-iqe^{2ika}+iqe^{-iqa}e^{ika}-2Qe^{2ika})=(iqe^{2ika}-iqe^{iqa}e^{ika}-2Qe^{2ika}-iqe^{-iqa}e^{ika}+iq+2Qe^{-iqa}e^{ika})</math>
+Pomnožimo celotno enačbo s členom <math>e^{-ika}</math>
+<math>(iqe^{iqa}-iqe^{-ika}+2Qe^{iqa}-iqe^{ika}+iqe^{-iqa}-2Qe^{ika})=(iqe^{ika}-iqe^{iqa}-2Qe^{ika}-iqe^{-iqa}+iqe^{-ika}+2Qe^{-iqa})</math>