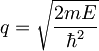Kronig-Penneyev model kristala

Iz Fizika trdne snovi 2007 - 2008

(Primerjava redakcij)

Redakcija: 00:15, 20 januar 2008

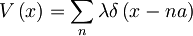
Imamo delec v 1D Kronig-Penneyevem potencialu: $V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)$

Iščemo lastne funkcije energije za ta sistem.

Potencial je več kot očitno periodičen: 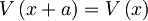$V\left(x+a\right)=V\left(x\right)$

Torej tudi za Hamiltonov operator: 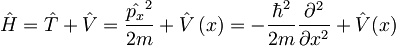$\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)$ velja, da je periodičen: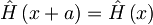 $\hat{H}\left(x+a\right)=\hat{H}\left(x\right)$

Uvedimo operator translacije: 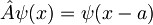$\hat{A}\psi(x)=\psi(x-a)$

Za lastne funkcije tega operatorja torej sledi: 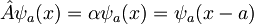$\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)$

Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza: 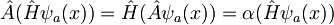$\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))$ .

Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: 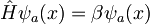$\hat{H}\psi_a(x)=\beta\psi_a(x)$

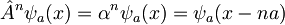
Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na. $\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)$

Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: $| α | = 1$ , torej jo lahko zapišemo kot $α = e - i φ$ oziroma, če to izrazimo s periodo a, kot $α = e - i k a$

Če sedaj povzamemo vse skupaj: $ψ a (x - a) = e - i k a ψ a (x)$ , oziroma $ψ a (x) e i k a = ψ a (x + a)$

Sedaj uporabimo sledeči nastavek: $ψ a (x) = e i k x u (x)$ , katerega nesemo v zgornjo enačbo: $e i k (x + a) u (x) = e i k (x + a) u (x + a)$ in od tod dobimo pogoj za funkcijo u(x): $u (x) = u (x + a)$ . Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala.

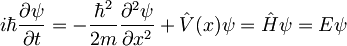
Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe: $i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi$

Rešitve v vmesnih področjih, kjer je V=0, so oblike

$ψ n (x) = A n e i q x + B n e - i q x = ψ n (x) = e i k x (A n e i (q - k) x + B n e - i (q + k) x) = e i k x u n (x)$ , kjer je $ψ n (x)$ lastna funkcija energije v n-tem področju in $q= \sqrt{\frac{2mE}{\hbar^2}}$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Kronig-Penneyev_model_kristala«

 Iščemo lastne funkcije energije za ta sistem.
+----
 Potencial je več kot očitno periodičen: <math>V\left(x+a\right)=V\left(x\right)</math>
 Če sedaj povzamemo vse skupaj: <math>\psi_a(x-a)=e^{-ika}\psi_a(x)</math>, oziroma <math>\psi_a(x)e^{ika}=\psi_a(x+a)</math>
+Sedaj uporabimo sledeči nastavek:<math>\psi_a(x)=e^{ikx}u(x)</math>, katerega nesemo v zgornjo enačbo: <math>e^{ik(x+a)}u(x)=e^{ik(x+a)}u(x+a)</math> in od tod dobimo pogoj za funkcijo ''u(x)'': <math>u(x)=u(x+a)</math>. Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala.
+----
+Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe:
+<math>i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi</math>
+Rešitve v vmesnih področjih, kjer je V=0, so oblike
+<math>\psi_n(x)=A_{n}e^{iqx}+B_{n}e^{-iqx}=\psi_n(x)=e^{ikx}(A_{n}e^{i(q-k)x}+B_{n}e^{-i(q+k)x})=e^{ikx}u_n(x)</math>, kjer je <math>\psi_n(x)</math> lastna funkcija energije v n-tem področju in <math>q= \sqrt{\frac{2mE}{\hbar^2}}</math>