Kronig-Penneyev model kristala

Iz Fizika trdne snovi 2007 - 2008

(Primerjava redakcij)

Redakcija: 23:22, 19 januar 2008

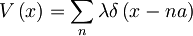
Imamo delec v 1D Kronig-Penneyevem potencialu: $V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)$

Iščemo lastne funkcije energije za ta sistem.

Potencial je več kot očitno periodičen: 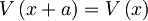$V\left(x+a\right)=V\left(x\right)$

Torej tudi za Hamiltonov operator: 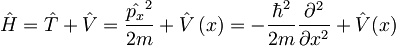$\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)$ velja, da je periodičen: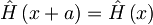 $\hat{H}\left(x+a\right)=\hat{H}\left(x\right)$

Uvedimo operator translacije: 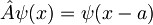$\hat{A}\psi(x)=\psi(x-a)$

Za lastne funkcije tega operatorja torej sledi: 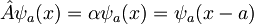$\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)$

Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza: 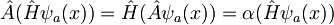$\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))$ .

Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: 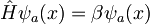$\hat{H}\psi_a(x)=\beta\psi_a(x)$

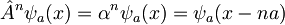
Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na. $\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)$

Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: $| α | = 1$ , torej jo lahko zapišemo kot $α = e - i φ$ oziroma, če to izrazimo s periodo a, kot $α = e - i k a$

Če sedaj povzamemo vse skupaj: $ψ a (x - a) = e - i k a ψ a (x)$ , oziroma $ψ a (x) e i k a = ψ a (x + a)$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Kronig-Penneyev_model_kristala«

 Za lastne funkcije tega operatorja torej sledi: <math>\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)</math>
-Ker  je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza: <math>\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))</math>.
+Ker  je Hamiltonov operator periodičen s periodo ''a'', komutira z operatorjem translacije, torej velja naslednja zveza: <math>\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))</math>.
-Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: <math>\hat{H}\psi_a(x)=k\psi_a(x)</math>
+Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: <math>\hat{H}\psi_a(x)=\beta\psi_a(x)</math>
+Sedaj lahko izvedemo ''n''-kratno translacijo tako, da ''n''-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za ''na''.
+<math>\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)</math>
+Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko ''n'' izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: <math>|\alpha|=1</math>, torej jo lahko zapišemo kot <math>\alpha=e^{-i\phi}</math> oziroma, če to izrazimo s periodo ''a'', kot <math>\alpha=e^{-ika}</math>
+Če sedaj povzamemo vse skupaj: <math>\psi_a(x-a)=e^{-ika}\psi_a(x)</math>, oziroma <math>\psi_a(x)e^{ika}=\psi_a(x+a)</math>