Kronig-Penneyev model kristala
Iz Fizika trdne snovi 2007 - 2008
(Primerjava redakcij)
| Redakcija: 15:14, 18 januar 2008 (spremeni) 87.119.143.25 (Pogovor) ← Pojdi na prejšnje urejanje |
Redakcija: 15:26, 18 januar 2008 (spremeni) (undo) 87.119.143.25 (Pogovor) Novejše urejanje → |
||
| Vrstica 6: | Vrstica 6: | ||
| Potencial je več kot očitno periodičen: <math>V\left(x+a\right)=V\left(x\right)</math> | Potencial je več kot očitno periodičen: <math>V\left(x+a\right)=V\left(x\right)</math> | ||
| - | Torej tudi za Hamiltonov operator: <math>H=T+V=\frac{p_x^2}{2m}+V\left(x\right) = | + | Torej tudi za Hamiltonov operator: <math>\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = |
| - | -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + V(x)</math> velja, da je periodičen: <math>H\left(x+a\right)=H\left(x\right)</math> | + | -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)</math> velja, da je periodičen: <math>\hat{H}\left(x+a\right)=\hat{H}\left(x\right)</math> |
| + | |||
| + | Uvedimo operator translacije | ||
Redakcija: 15:26, 18 januar 2008
Imamo delec v 1D Kronig-Penneyevem potencialu:
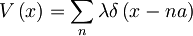
Iščemo lastne funkcije energije za ta sistem.
Potencial je več kot očitno periodičen: 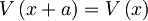
Torej tudi za Hamiltonov operator: 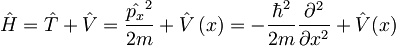 velja, da je periodičen:
velja, da je periodičen: 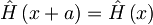
Uvedimo operator translacije