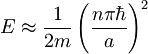Kronig-Penneyev model kristala

Iz Fizika trdne snovi 2007 - 2008

(Primerjava redakcij)

Skoči na: navigacija, iskanje

Trenutna redakcija

[spremeni] Naloga

Imamo delec v 1D Kronig-Penneyevem potencialu:

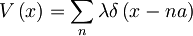
$V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)$

Iščemo lastne funkcije energije za ta sistem.

[spremeni] Rešitev

Potencial je več kot očitno periodičen:

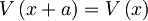
$V\left(x+a\right)=V\left(x\right)$

Torej tudi za Hamiltonov operator velja, da je periodičen:

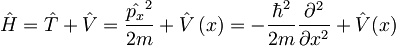
$\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)$

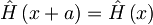
$\hat{H}\left(x+a\right)=\hat{H}\left(x\right)$

Uvedimo operator translacije:

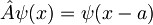
$\hat{A}\psi(x)=\psi(x-a)$

Za lastne funkcije tega operatorja torej sledi:

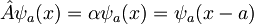
$\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)$

Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza:

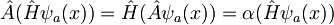$\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))$ .

Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja:

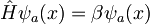
$\hat{H}\psi_a(x)=\beta\psi_a(x)$

Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na.

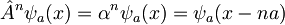
$\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)$

Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: $| α | = 1$ , torej jo lahko zapišemo kot

$α = e - i φ$

oziroma, če to izrazimo s periodo a, kot

$α = e - i k a$

Če sedaj povzamemo vse skupaj:

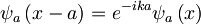
$\psi_a\left(x-a\right)=e^{-ika}\psi_a\left(x\right)$

oziroma

$\psi_a\left(x\right)e^{ika}=\psi_a\left(x+a\right)$

Sedaj uporabimo sledeči nastavek:

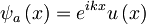
$\psi_a\left(x\right)=e^{ikx}u\left(x\right)$

katerega nesemo v zgornjo enačbo:

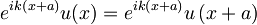
$e^{ik\left(x+a\right)}u(x)=e^{ik\left(x+a\right)}u\left(x+a\right)$

in od tod dobimo pogoj za funkcijo u(x):

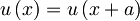
$u\left(x\right)=u\left(x+a\right)$

Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala.

Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe:

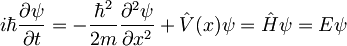
$i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi$

Rešitve v vmesnih področjih, kjer je V=0, so oblike

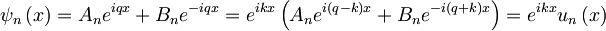
$\psi_n\left(x\right)=A_{n}e^{iqx}+B_{n}e^{-iqx}=e^{ikx}\left(A_{n}e^{i(q-k)x}+B_{n}e^{-i(q+k)x}\right)=e^{ikx}u_n\left(x\right)$

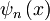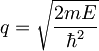
kjer je $\psi_n\left(x\right)$ lastna funkcija energije v n-tem področju in $q= \sqrt{\frac{2mE}{\hbar^2}}$

Sedaj nesemo dobljeni izraz za u(x) v pogoj, dobljen iz periodičnosti potenciala: u(x)=u(x+a):

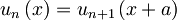
$u_n\left(x\right)=u_{n+1}\left(x+a\right)$

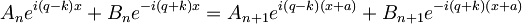
$A_{n}e^{i\left(q-k\right)x}+B_{n}e^{-i\left(q+k\right)x}=A_{n+1}e^{i\left(q-k\right)\left(x+a\right)}+B_{n+1}e^{-i\left(q+k\right)\left(x+a\right)}$

Ker to velja za vsak x, sledi:

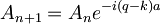
$A_{n+1}=A_{n}e^{-i\left(q-k\right)a}$

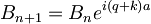
$B_{n+1}=B_{n}e^{i\left(q+k\right)a}$

torej

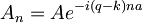
$A_{n}=Ae^{-i\left(q-k\right)na}$

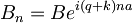
$B_{n}=Be^{i\left(q+k\right)na}$

kjer sta: $A = A 0$ in $B = B 0$

Torej lahko zapišemo rešitev Schrodingerjeve enačbe za n-to področje kot:

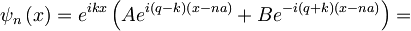
$\psi_n\left(x\right)=e^{ikx}\left(Ae^{i\left(q-k\right)\left(x-na\right)}+Be^{-i\left(q+k\right)\left(x-na\right)}\right)=$

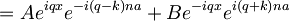
$=Ae^{iqx}e^{-i\left(q-k\right)na}+Be^{-iqx}e^{i\left(q+k\right)na}$

Neznane količine: q (in torej tudi lastne energije E), A in B, dobimo iz začetnih in robnih pogojev.

Robni pogoji:

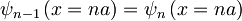
1.) $\psi_{n-1}\left(x=na\right)=\psi_{n}\left(x=na\right)$

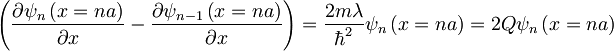
2.) $\left(\frac{\partial\psi_{n}\left(x=na\right)}{\partial{x}}-\frac{\partial\psi_{n-1}\left(x=na\right)}{\partial{x}}\right)=\frac{2m\lambda}{\hbar^2}\psi_{n}\left(x=na\right)=2Q\psi_{n}\left(x=na\right)$

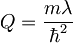
kjer je $Q=\frac{m\lambda}{\hbar^2}$

Ko vstavimo valovno funkcijo v prvi robni pogoj, dobimo:

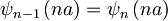
$\psi_{n-1}\left(na\right)=\psi_{n}\left(na\right)$

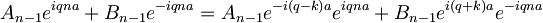
$A_{n-1}e^{iqna}+B_{n-1}e^{-iqna}=A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}+B_{n-1}e^{i\left(q+k\right)a}e^{-iqna}$

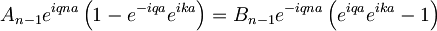
$A_{n-1}e^{iqna}\left(1-e^{-iqa}e^{ika}\right)=B_{n-1}e^{-iqna}\left(e^{iqa}e^{ika}-1\right)$

Iz drugega robnega pogoja pa dobimo:

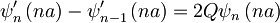
$\psi_{n}'\left(na\right)-\psi_{n-1}'\left(na\right)=2Q\psi_{n}\left(na\right)$

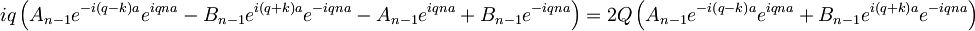
$iq\left(A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}-B_{n-1}e^{i\left(q+k\right)a}e^{-iqna}-A_{n-1}e^{iqna}+B_{n-1}e^{-iqna}\right)=2Q\left(A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}+B_{n-1}e^{i\left(q+k\right)a}e^{-iqna}\right)$

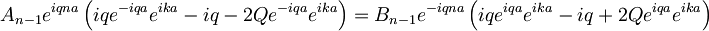
$A_{n-1}e^{iqna}\left(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika}\right)=B_{n-1}e^{-iqna}\left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}\right)$

Sedaj lahko med seboj zdelimo obe enačbi, ki sledita iz robnih pogojev, ter se tako znebimo konstant A in B

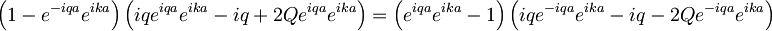
$\left(1-e^{-iqa}e^{ika}\right)\left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}\right)=\left(e^{iqa}e^{ika}-1\right)\left(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika}\right)$

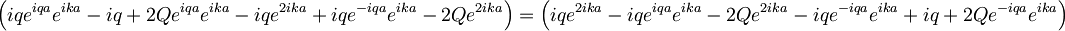
$\left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}-iqe^{2ika}+iqe^{-iqa}e^{ika}-2Qe^{2ika}\right)=\left(iqe^{2ika}-iqe^{iqa}e^{ika}-2Qe^{2ika}-iqe^{-iqa}e^{ika}+iq+2Qe^{-iqa}e^{ika}\right)$

Pomnožimo celotno enačbo s členom $e - i k a$ :

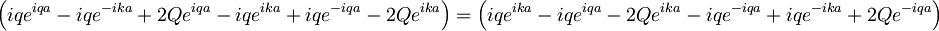
$\left(iqe^{iqa}-iqe^{-ika}+2Qe^{iqa}-iqe^{ika}+iqe^{-iqa}-2Qe^{ika}\right)=\left(iqe^{ika}-iqe^{iqa}-2Qe^{ika}-iqe^{-iqa}+iqe^{-ika}+2Qe^{-iqa}\right)$

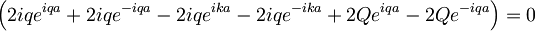
$\left(2iqe^{iqa}+2iqe^{-iqa}-2iqe^{ika}-2iqe^{-ika}+2Qe^{iqa}-2Qe^{-iqa}\right)=0$

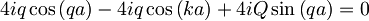
$4iq\cos\left(qa\right)-4iq\cos\left(ka\right)+4iQ\sin\left(qa\right)=0$

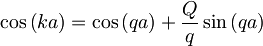
$\cos\left(ka\right)=\cos\left(qa\right)+\frac{Q}{q}\sin\left(qa\right)$

Prišli smo do enačbe, ki povezuje "valovni vektor" k s konstanto 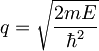$q= \sqrt{\frac{2mE}{\hbar^2}}$ . Q je tu le parameter, odvisen od višine potenciala $λ$ in mase delca m.

Analizirajmo sedaj to rešitev in poglejmo kakšne energije ji ustrezajo.

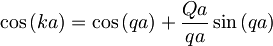
$\cos\left(ka\right)=\cos\left(qa\right)+\frac{Qa}{qa}\sin\left(qa\right)$

Leva stran enačbe je omejena z vrednostima +1 in -1, medtem, ko za desno stran to očitno ne velja. Za majhne vrednosti parametra qa gre faktor 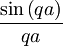$\frac{\sin\left(qa\right)}{qa}$ proti 1, prav tako pa tudi člen $cos(q a)$ , zato celotna desna stran v tem pasu presega vrednost +1 in to ne glede na (pozitivno) vrednost parametra Qa.

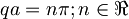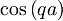Težave se pojavijo tudi v okolici točk $qa=n\pi; n \in \Re$ . Tam lahko člen $\cos\left(qa\right)$ precej dobro aproximiramo s parabolo, medtem, ko ima člen 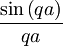$\frac{\sin\left(qa\right)}{qa}$ tam ničle in ga smemo razviti le do linearnega člena, kar pomeni, da v bližnji okolici teh točk ta člen prevlada in desna stran zgornje enačbe po absolutni vrednosti preseže 1.

Ta rezultat interpretiramo tako, da imamo tam prepovedane pasove - v teh območjih energije (qa) enačba nima rešitev. Prepovedani energijski pasovi ustrezajo energijam: $E\approx\frac{1}{2m}\left(\frac{n\pi\hbar}{a}\right)^2$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Kronig-Penneyev_model_kristala«

-EUwHQf  <a href="http://neetgvtafqfx.com/">neetgvtafqfx</a>, [url=http://xasacepqkdxs.com/]xasacepqkdxs[/url], [link=http://gxohxeegetxm.com/]gxohxeegetxm[/link], http://wafzlqljilmt.com/
+== Naloga==
+Imamo delec v 1D Kronig-Penneyevem potencialu:
+<math>
+V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)
+</math>
+Iščemo lastne funkcije energije za ta sistem.
 == Rešitev ==