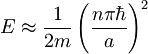Kronig-Penneyev model kristala
Iz Fizika trdne snovi 2007 - 2008
| Redakcija: 21:20, 21 januar 2008 (spremeni) 195.210.234.108 (Pogovor) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (20:14, 18 november 2008) (spremeni) (undo) Asistent (Pogovor | prispevki) m (vrnitev sprememb uporabnika »194.208.246.163« (pogovor) na zadnje urejanje uporabnika »195.210.234.108«) |
||
| ( not shown.) | |||
| Vrstica 1: | Vrstica 1: | ||
| + | == Naloga== | ||
| + | |||
| + | |||
| Imamo delec v 1D Kronig-Penneyevem potencialu: | Imamo delec v 1D Kronig-Penneyevem potencialu: | ||
| - | <math>V\left(x\right)=\sum_n\lambda\delta\left(x-na\right)</math> | + | |
| + | <math> | ||
| + | V\left(x\right)=\sum_n\lambda\delta\left(x-na\right) | ||
| + | </math> | ||
| Iščemo lastne funkcije energije za ta sistem. | Iščemo lastne funkcije energije za ta sistem. | ||
| - | ---- | ||
| - | Potencial je več kot očitno periodičen: <math>V\left(x+a\right)=V\left(x\right)</math> | + | == Rešitev == |
| - | Torej tudi za Hamiltonov operator: <math>\hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = | ||
| - | -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x)</math> velja, da je periodičen: <math>\hat{H}\left(x+a\right)=\hat{H}\left(x\right)</math> | ||
| - | Uvedimo operator translacije: <math>\hat{A}\psi(x)=\psi(x-a)</math> | + | Potencial je več kot očitno periodičen: |
| - | Za lastne funkcije tega operatorja torej sledi: <math>\hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a)</math> | + | <math> |
| + | V\left(x+a\right)=V\left(x\right) | ||
| + | </math> | ||
| - | Ker je Hamiltonov operator periodičen s periodo ''a'', komutira z operatorjem translacije, torej velja naslednja zveza: <math>\hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x))</math>. | + | Torej tudi za Hamiltonov operator velja, da je periodičen: |
| - | Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: <math>\hat{H}\psi_a(x)=\beta\psi_a(x)</math> | + | <math> |
| + | \hat{H}=\hat{T}+\hat{V}=\frac{\hat{p_x}^2}{2m}+\hat{V}\left(x\right) = | ||
| + | -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial{x}^2} + \hat{V}(x) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \hat{H}\left(x+a\right)=\hat{H}\left(x\right) | ||
| + | </math> | ||
| + | |||
| + | Uvedimo operator translacije: | ||
| + | |||
| + | <math> | ||
| + | \hat{A}\psi(x)=\psi(x-a) | ||
| + | </math> | ||
| + | |||
| + | Za lastne funkcije tega operatorja torej sledi: | ||
| + | |||
| + | <math> | ||
| + | \hat{A}\psi_a(x)=\alpha\psi_a(x)=\psi_a(x-a) | ||
| + | </math> | ||
| + | |||
| + | Ker je Hamiltonov operator periodičen s periodo ''a'', komutira z operatorjem translacije, torej velja naslednja zveza: | ||
| + | |||
| + | <math> | ||
| + | \hat{A}(\hat{H}\psi_a(x))=\hat{H}(\hat{A}\psi_a(x))=\alpha(\hat{H}\psi_a(x)) | ||
| + | </math>. | ||
| + | |||
| + | Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja: | ||
| + | |||
| + | <math> | ||
| + | \hat{H}\psi_a(x)=\beta\psi_a(x) | ||
| + | </math> | ||
| Sedaj lahko izvedemo ''n''-kratno translacijo tako, da ''n''-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za ''na''. | Sedaj lahko izvedemo ''n''-kratno translacijo tako, da ''n''-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za ''na''. | ||
| - | <math>\hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na)</math> | ||
| - | Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko ''n'' izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: <math>|\alpha|=1</math>, torej jo lahko zapišemo kot <math>\alpha=e^{-i\phi}</math> oziroma, če to izrazimo s periodo ''a'', kot <math>\alpha=e^{-ika}</math> | + | <math> |
| + | \hat{A}^n\psi_a(x)=\alpha^n\psi_a(x)=\psi_a(x-na) | ||
| + | </math> | ||
| - | Če sedaj povzamemo vse skupaj: <math>\psi_a(x-a)=e^{-ika}\psi_a(x)</math>, oziroma <math>\psi_a(x)e^{ika}=\psi_a(x+a)</math> | + | Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko ''n'' izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: <math>|\alpha|=1</math>, torej jo lahko zapišemo kot |
| - | Sedaj uporabimo sledeči nastavek:<math>\psi_a(x)=e^{ikx}u(x)</math>, katerega nesemo v zgornjo enačbo: <math>e^{ik(x+a)}u(x)=e^{ik(x+a)}u(x+a)</math> in od tod dobimo pogoj za funkcijo ''u(x)'': <math>u(x)=u(x+a)</math>. Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala. | + | <math> |
| + | \alpha=e^{-i\phi} | ||
| + | </math> | ||
| + | |||
| + | oziroma, če to izrazimo s periodo ''a'', kot | ||
| + | |||
| + | <math> | ||
| + | \alpha=e^{-ika} | ||
| + | </math> | ||
| + | |||
| + | Če sedaj povzamemo vse skupaj: | ||
| + | |||
| + | <math> | ||
| + | \psi_a\left(x-a\right)=e^{-ika}\psi_a\left(x\right) | ||
| + | </math> | ||
| + | |||
| + | oziroma | ||
| + | |||
| + | <math> | ||
| + | \psi_a\left(x\right)e^{ika}=\psi_a\left(x+a\right) | ||
| + | </math> | ||
| + | |||
| + | Sedaj uporabimo sledeči nastavek: | ||
| + | |||
| + | <math> | ||
| + | \psi_a\left(x\right)=e^{ikx}u\left(x\right) | ||
| + | </math> | ||
| + | |||
| + | katerega nesemo v zgornjo enačbo: | ||
| + | |||
| + | <math> | ||
| + | e^{ik\left(x+a\right)}u(x)=e^{ik\left(x+a\right)}u\left(x+a\right) | ||
| + | </math> | ||
| + | |||
| + | in od tod dobimo pogoj za funkcijo ''u(x)'': | ||
| + | |||
| + | <math> | ||
| + | u\left(x\right)=u\left(x+a\right) | ||
| + | </math> | ||
| + | |||
| + | Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala. | ||
| ---- | ---- | ||
| Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe: | Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe: | ||
| - | <math>i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi</math> | + | |
| + | <math> | ||
| + | i\hbar\frac{\partial\psi}{\partial{t}}=-\frac{\hbar^2}{2m} \frac{\partial^2\psi}{\partial{x}^2} + \hat{V}(x)\psi=\hat{H}\psi=E\psi | ||
| + | </math> | ||
| Rešitve v vmesnih področjih, kjer je V=0, so oblike | Rešitve v vmesnih področjih, kjer je V=0, so oblike | ||
| - | <math>\psi_n(x)=A_{n}e^{iqx}+B_{n}e^{-iqx}=\psi_n(x)=e^{ikx}(A_{n}e^{i(q-k)x}+B_{n}e^{-i(q+k)x})=e^{ikx}u_n(x)</math>, kjer je <math>\psi_n(x)</math> lastna funkcija energije v n-tem področju in <math>q= \sqrt{\frac{2mE}{\hbar^2}}</math> | + | <math> |
| + | \psi_n\left(x\right)=A_{n}e^{iqx}+B_{n}e^{-iqx}=e^{ikx}\left(A_{n}e^{i(q-k)x}+B_{n}e^{-i(q+k)x}\right)=e^{ikx}u_n\left(x\right) | ||
| + | </math> | ||
| + | |||
| + | kjer je | ||
| + | <math> | ||
| + | \psi_n\left(x\right) | ||
| + | </math> | ||
| + | lastna funkcija energije v n-tem področju in | ||
| + | <math> | ||
| + | q= \sqrt{\frac{2mE}{\hbar^2}} | ||
| + | </math> | ||
| Sedaj nesemo dobljeni izraz za ''u(x)'' v pogoj, dobljen iz periodičnosti potenciala: ''u(x)=u(x+a)'': | Sedaj nesemo dobljeni izraz za ''u(x)'' v pogoj, dobljen iz periodičnosti potenciala: ''u(x)=u(x+a)'': | ||
| - | <math>u_n(x)=u_{n+1}(x+a)</math> | + | <math> |
| + | u_n\left(x\right)=u_{n+1}\left(x+a\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | A_{n}e^{i\left(q-k\right)x}+B_{n}e^{-i\left(q+k\right)x}=A_{n+1}e^{i\left(q-k\right)\left(x+a\right)}+B_{n+1}e^{-i\left(q+k\right)\left(x+a\right)}</math> | ||
| + | |||
| + | Ker to velja za vsak ''x'', sledi: | ||
| + | |||
| + | <math> | ||
| + | A_{n+1}=A_{n}e^{-i\left(q-k\right)a} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | B_{n+1}=B_{n}e^{i\left(q+k\right)a} | ||
| + | </math> | ||
| + | |||
| + | torej | ||
| + | |||
| + | <math> | ||
| + | A_{n}=Ae^{-i\left(q-k\right)na} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | B_{n}=Be^{i\left(q+k\right)na} | ||
| + | </math> | ||
| + | |||
| + | kjer sta: | ||
| + | <math> | ||
| + | A =A_0 | ||
| + | </math> in | ||
| + | <math> | ||
| + | B =B_0 | ||
| + | </math> | ||
| + | |||
| + | Torej lahko zapišemo rešitev Schrodingerjeve enačbe za ''n''-to področje kot: | ||
| + | |||
| + | <math> | ||
| + | \psi_n\left(x\right)=e^{ikx}\left(Ae^{i\left(q-k\right)\left(x-na\right)}+Be^{-i\left(q+k\right)\left(x-na\right)}\right)= | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | =Ae^{iqx}e^{-i\left(q-k\right)na}+Be^{-iqx}e^{i\left(q+k\right)na} | ||
| + | </math> | ||
| + | |||
| + | Neznane količine: ''q'' (in torej tudi lastne energije ''E''), ''A'' in ''B'', dobimo iz začetnih in robnih pogojev. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Robni pogoji:''' | ||
| + | |||
| + | 1.) <math> | ||
| + | \psi_{n-1}\left(x=na\right)=\psi_{n}\left(x=na\right) | ||
| + | </math> | ||
| + | |||
| + | 2.) <math> | ||
| + | \left(\frac{\partial\psi_{n}\left(x=na\right)}{\partial{x}}-\frac{\partial\psi_{n-1}\left(x=na\right)}{\partial{x}}\right)=\frac{2m\lambda}{\hbar^2}\psi_{n}\left(x=na\right)=2Q\psi_{n}\left(x=na\right) | ||
| + | </math> | ||
| + | |||
| + | kjer je | ||
| + | <math> | ||
| + | Q=\frac{m\lambda}{\hbar^2} | ||
| + | </math> | ||
| + | |||
| + | Ko vstavimo valovno funkcijo v prvi robni pogoj, dobimo: | ||
| + | |||
| + | <math> | ||
| + | \psi_{n-1}\left(na\right)=\psi_{n}\left(na\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | A_{n-1}e^{iqna}+B_{n-1}e^{-iqna}=A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}+B_{n-1}e^{i\left(q+k\right)a}e^{-iqna} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | A_{n-1}e^{iqna}\left(1-e^{-iqa}e^{ika}\right)=B_{n-1}e^{-iqna}\left(e^{iqa}e^{ika}-1\right) | ||
| + | </math> | ||
| + | |||
| + | Iz drugega robnega pogoja pa dobimo: | ||
| + | |||
| + | <math> | ||
| + | \psi_{n}'\left(na\right)-\psi_{n-1}'\left(na\right)=2Q\psi_{n}\left(na\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | iq\left(A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}-B_{n-1}e^{i\left(q+k\right)a}e^{-iqna}-A_{n-1}e^{iqna}+B_{n-1}e^{-iqna}\right)=2Q\left(A_{n-1}e^{-i\left(q-k\right)a}e^{iqna}+B_{n-1}e^{i\left(q+k\right)a}e^{-iqna}\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | A_{n-1}e^{iqna}\left(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika}\right)=B_{n-1}e^{-iqna}\left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}\right) | ||
| + | </math> | ||
| + | |||
| + | Sedaj lahko med seboj zdelimo obe enačbi, ki sledita iz robnih pogojev, ter se tako znebimo konstant ''A'' in ''B'' | ||
| + | |||
| + | <math> | ||
| + | \left(1-e^{-iqa}e^{ika}\right)\left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}\right)=\left(e^{iqa}e^{ika}-1\right)\left(iqe^{-iqa}e^{ika}-iq-2Qe^{-iqa}e^{ika}\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \left(iqe^{iqa}e^{ika}-iq+2Qe^{iqa}e^{ika}-iqe^{2ika}+iqe^{-iqa}e^{ika}-2Qe^{2ika}\right)=\left(iqe^{2ika}-iqe^{iqa}e^{ika}-2Qe^{2ika}-iqe^{-iqa}e^{ika}+iq+2Qe^{-iqa}e^{ika}\right)</math> | ||
| + | |||
| + | Pomnožimo celotno enačbo s členom | ||
| + | <math> | ||
| + | e^{-ika} | ||
| + | </math>: | ||
| + | |||
| + | <math> | ||
| + | \left(iqe^{iqa}-iqe^{-ika}+2Qe^{iqa}-iqe^{ika}+iqe^{-iqa}-2Qe^{ika}\right)=\left(iqe^{ika}-iqe^{iqa}-2Qe^{ika}-iqe^{-iqa}+iqe^{-ika}+2Qe^{-iqa}\right) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \left(2iqe^{iqa}+2iqe^{-iqa}-2iqe^{ika}-2iqe^{-ika}+2Qe^{iqa}-2Qe^{-iqa}\right)=0 | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | 4iq\cos\left(qa\right)-4iq\cos\left(ka\right)+4iQ\sin\left(qa\right)=0 | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \cos\left(ka\right)=\cos\left(qa\right)+\frac{Q}{q}\sin\left(qa\right) | ||
| + | </math> | ||
| + | |||
| + | Prišli smo do enačbe, ki povezuje "valovni vektor" ''k'' s konstanto | ||
| + | <math> | ||
| + | q= \sqrt{\frac{2mE}{\hbar^2}} | ||
| + | </math>. | ||
| + | ''Q'' je tu le parameter, odvisen od višine potenciala | ||
| + | <math> | ||
| + | \lambda | ||
| + | </math> in mase delca ''m''. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Analizirajmo sedaj to rešitev in poglejmo kakšne energije ji ustrezajo. | ||
| + | |||
| + | <math> | ||
| + | \cos\left(ka\right)=\cos\left(qa\right)+\frac{Qa}{qa}\sin\left(qa\right) | ||
| + | </math> | ||
| + | |||
| + | Leva stran enačbe je omejena z vrednostima +1 in -1, medtem, ko za desno stran to očitno ne velja. Za majhne vrednosti parametra ''qa'' gre faktor | ||
| + | <math> | ||
| + | \frac{\sin\left(qa\right)}{qa} | ||
| + | </math> | ||
| + | proti 1, prav tako pa tudi člen <math>\cos(qa)</math>, zato celotna desna stran v tem pasu presega vrednost +1 in to ne glede na (pozitivno) vrednost parametra ''Qa''. | ||
| + | |||
| + | Težave se pojavijo tudi v okolici točk | ||
| + | <math> | ||
| + | qa=n\pi; n \in \Re | ||
| + | </math>. | ||
| + | Tam lahko člen | ||
| + | <math> | ||
| + | \cos\left(qa\right) | ||
| + | </math> | ||
| + | precej dobro aproximiramo s parabolo, medtem, ko ima člen | ||
| + | <math> | ||
| + | \frac{\sin\left(qa\right)}{qa} | ||
| + | </math> | ||
| + | tam ničle in ga smemo razviti le do linearnega člena, kar pomeni, da v bližnji okolici teh točk ta člen prevlada in desna stran zgornje enačbe po absolutni vrednosti preseže 1. | ||
| - | <math>A_{n}e^{i(q-k)x}+B_{n}e^{-i(q+k)x}=A_{n+1}e^{i(q-k)(x+a)}+B_{n+1}e^{-i(q+k)(x+a)}</math>, | + | Ta rezultat interpretiramo tako, da imamo tam prepovedane pasove - v teh območjih energije ''(qa)'' enačba nima rešitev. Prepovedani energijski pasovi ustrezajo energijam: <math> |
| + | E\approx\frac{1}{2m}\left(\frac{n\pi\hbar}{a}\right)^2 | ||
| + | </math> | ||
Trenutna redakcija
[spremeni] Naloga
Imamo delec v 1D Kronig-Penneyevem potencialu:
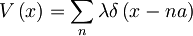
Iščemo lastne funkcije energije za ta sistem.
[spremeni] Rešitev
Potencial je več kot očitno periodičen:
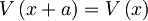
Torej tudi za Hamiltonov operator velja, da je periodičen:
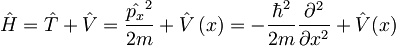
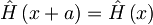
Uvedimo operator translacije:
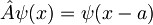
Za lastne funkcije tega operatorja torej sledi:
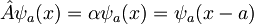
Ker je Hamiltonov operator periodičen s periodo a, komutira z operatorjem translacije, torej velja naslednja zveza:
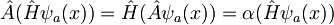 .
.
Od tod sledi, da so lastne funkcije operatorja translacije hkrati tudi lastne fukcije Hamiltonovega operatorja:
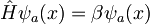
Sedaj lahko izvedemo n-kratno translacijo tako, da n-krat delujemo na funkcijo z operatorjem translacije. Temu ustreza premik valovne fukcije za na.
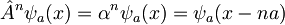
Ker vemo, da je verjetnost, da tam najdemo delec končna in od nič različna in ker imamo neskončen kristal (torej lahko n izberemo poljubno velik), dobimo od tod pogoj za lastno vrednost operatorja translacije kot: | α | = 1, torej jo lahko zapišemo kot
α = e − iφ
oziroma, če to izrazimo s periodo a, kot
α = e − ika
Če sedaj povzamemo vse skupaj:
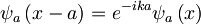
oziroma

Sedaj uporabimo sledeči nastavek:
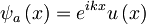
katerega nesemo v zgornjo enačbo:
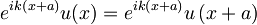
in od tod dobimo pogoj za funkcijo u(x):
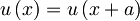
Toliko nam lahko da sama simetrija problema - torej periodičnost potenciala.
Lastne funkcije poiščemo s pomočjo Schrodingerjeve enačbe:
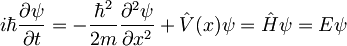
Rešitve v vmesnih področjih, kjer je V=0, so oblike
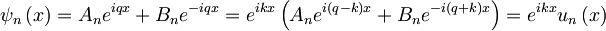
kjer je
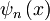 lastna funkcija energije v n-tem področju in
lastna funkcija energije v n-tem področju in
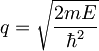
Sedaj nesemo dobljeni izraz za u(x) v pogoj, dobljen iz periodičnosti potenciala: u(x)=u(x+a):
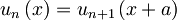
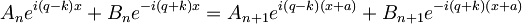
Ker to velja za vsak x, sledi:
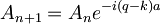
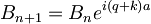
torej
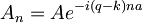
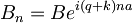
kjer sta: A = A0 in B = B0
Torej lahko zapišemo rešitev Schrodingerjeve enačbe za n-to področje kot:
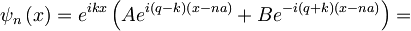
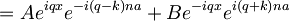
Neznane količine: q (in torej tudi lastne energije E), A in B, dobimo iz začetnih in robnih pogojev.
Robni pogoji:
1.) 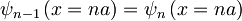
2.) 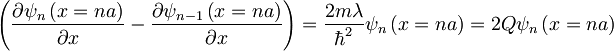
kjer je
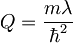
Ko vstavimo valovno funkcijo v prvi robni pogoj, dobimo:
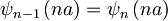
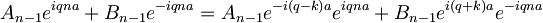
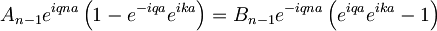
Iz drugega robnega pogoja pa dobimo:
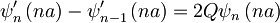
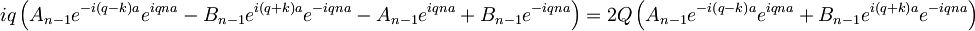
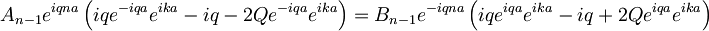
Sedaj lahko med seboj zdelimo obe enačbi, ki sledita iz robnih pogojev, ter se tako znebimo konstant A in B
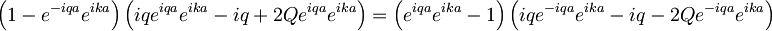
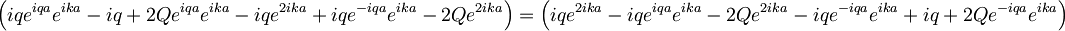
Pomnožimo celotno enačbo s členom e − ika:
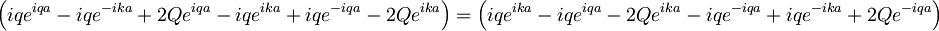
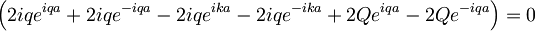
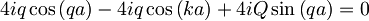
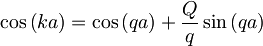
Prišli smo do enačbe, ki povezuje "valovni vektor" k s konstanto
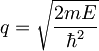 .
Q je tu le parameter, odvisen od višine potenciala
λ in mase delca m.
.
Q je tu le parameter, odvisen od višine potenciala
λ in mase delca m.
Analizirajmo sedaj to rešitev in poglejmo kakšne energije ji ustrezajo.
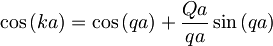
Leva stran enačbe je omejena z vrednostima +1 in -1, medtem, ko za desno stran to očitno ne velja. Za majhne vrednosti parametra qa gre faktor
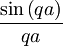 proti 1, prav tako pa tudi člen cos(qa), zato celotna desna stran v tem pasu presega vrednost +1 in to ne glede na (pozitivno) vrednost parametra Qa.
proti 1, prav tako pa tudi člen cos(qa), zato celotna desna stran v tem pasu presega vrednost +1 in to ne glede na (pozitivno) vrednost parametra Qa.
Težave se pojavijo tudi v okolici točk
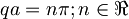 .
Tam lahko člen
.
Tam lahko člen
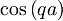 precej dobro aproximiramo s parabolo, medtem, ko ima člen
precej dobro aproximiramo s parabolo, medtem, ko ima člen
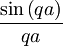 tam ničle in ga smemo razviti le do linearnega člena, kar pomeni, da v bližnji okolici teh točk ta člen prevlada in desna stran zgornje enačbe po absolutni vrednosti preseže 1.
tam ničle in ga smemo razviti le do linearnega člena, kar pomeni, da v bližnji okolici teh točk ta člen prevlada in desna stran zgornje enačbe po absolutni vrednosti preseže 1.
Ta rezultat interpretiramo tako, da imamo tam prepovedane pasove - v teh območjih energije (qa) enačba nima rešitev. Prepovedani energijski pasovi ustrezajo energijam: