Meritev

Iz Kvantna mehanika I 2010 - 2011

(Primerjava redakcij)

Asistent (Pogovor | prispevki)
(Nova stran: Obravnavaj delec v harmonskem oscilatorju. Ob <math>t=0</math> je delec v stanju <math>|D\rangle=(|0\rangle+|1\rangle)/\sqrt{2}</math>, v katerem je verjetnostna gostota v območju <math...)
Novejše urejanje →

Redakcija: 12:47, 23. november 2010

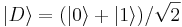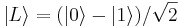Obravnavaj delec v harmonskem oscilatorju. Ob $t = 0$ je delec v stanju $|D\rangle=(|0\rangle+|1\rangle)/\sqrt{2}$ , v katerem je verjetnostna gostota v območju $x > 0$ večja kot v območju $x < 0$ . Obratno velja za stanje $|L\rangle=(|0\rangle-|1\rangle)/\sqrt{2}$ .

Izračunaj časovni razvoj valovne funkcije delca.
Kolikšna je verjetnost, da se po meritvi ob času $t$ delec nahaja v levem (desnem) delu potencialne jame? V kakšnem stanju je delec takoj po meritvi v vsakem od obeh primerov?
Kako na meritev ob času t vpliva dodatna meritev ob času t / 2, če
1. poznamo rezultat te meritve?
2. rezultata te meritve ne poznamo?