Časovno odvisna perturbacija
Iz Kvantna mehanika I 2009 - 2010
(Primerjava redakcij)
(Nova stran: Vodikov atom je v homogenem električnem polju <math>E(t)=E_0\frac{1}{1+\left(\frac{t}{\tau}\right)^2}</math>. Kolikšna je verjetnost, daje atom ob <math>t=\infty</math> v prvem vzbu...) |
(Nova stran: Vodikov atom je v homogenem električnem polju <math>E(t)=E_0\frac{1}{1+\left(\frac{t}{\tau}\right)^2}</math>. Kolikšna je verjetnost, daje atom ob <math>t=\infty</math> v prvem vzbu...) |
Current revision as of 11:06, 19. maj 2010
Vodikov atom je v homogenem električnem polju
.
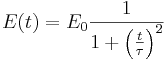Kolikšna je verjetnost, daje atom ob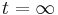 
v prvem vzbujenem stanju, če je bil ob 
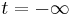v osnovnem stanju? Pri katerem τ je ta verjetnost največja? Predpostavi, da je električno polje dovolj šibko, da lahko uporabiš perturbacijsko teorijo.