Meritev
Iz Kvantna mehanika I 2009 - 2010
(Primerjava redakcij)
(Nova stran: Obravnavaj delec v harmonskem oscilatorju. Ob <math>t=0</math> je delec v stanju <math>|D\rangle=(|0\rangle+|1\rangle)/\sqrt{2}</math>, v katerem je verjetnostna gostota v območju <math...) |
(Nova stran: Obravnavaj delec v harmonskem oscilatorju. Ob <math>t=0</math> je delec v stanju <math>|D\rangle=(|0\rangle+|1\rangle)/\sqrt{2}</math>, v katerem je verjetnostna gostota v območju <math...) |
Current revision as of 11:19, 1. april 2010
Obravnavaj delec v harmonskem oscilatorju. Ob t = 0 je delec v stanju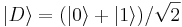 
, v katerem je verjetnostna gostota v območju x > 0 večja kot v območju x < 0. Obratno velja za stanje 
.
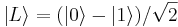- Izračunaj časovni razvoj valovne funkcije delca.
- Kolikšna je verjetnost, da se po meritvi ob času t delec nahaja v levem (desnem) delu potencialne jame? V kakšnem stanju je delec takoj po meritvi v vsakem od obeh primerov?
- Kolikšna je verjetnost, da se po meritvi ob času t delec nahaja v levem (desnem) delu potencialne jame, če smo pred tem opravili enako meritev ob časih
, 
, ..., 
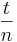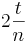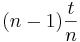, kjer gre 
?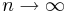