Koherentna stanja harmonskega oscilatorja I

Iz Kvantna Mehanika I 2006 - 2007

Skoči na: navigacija, iskanje

Vsebina

Naloga

Za delec v koherentnem stanju 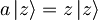a\left|z\right\rangle=z\left|z\right\rangle harmonskega oscilatorja 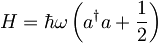H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right) izračunaj nedoločenosti položaja, gibalne količine in energije.

Rešitev

Nedoločenost koordinate

Lego opišemo z

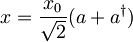x=\frac{x_{0}}{\sqrt{2}}(a+a^\dagger), kjer je

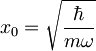x_{0}=\sqrt{\frac{\hbar}{m\omega}}.

Povprečna vrednost lege:

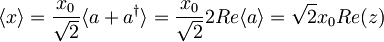\langle x\rangle=\frac{x_{0}}{\sqrt{2}}\langle a+a^\dagger\rangle=\frac{x_{0}}{\sqrt{2}}2 Re \langle a\rangle=\sqrt{2}x_{0}Re(z),

zadnji korak pojasni zveza:

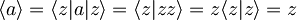\langle a \rangle= \langle z |a|z\rangle=\langle z|zz \rangle=z\langle z|z \rangle=z.

Povprečna vrednost kvadrata lege:

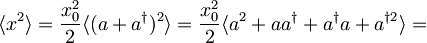
\langle x^2\rangle = \frac{x_{0}^2}{2}\langle (a+a^\dagger)^2\rangle= \frac{x_{0}^2}{2}\langle a^2+aa^\dagger+a^\dagger a + a^{\dagger 2}\rangle=

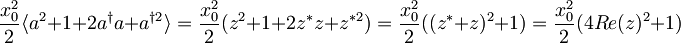
\frac{x_{0}^{2}}{2}\langle a^2+1+2a^\dagger a+a^{\dagger 2}\rangle= \frac{x_{0}^{2}}{2}(z^2+1+2z^*z+z^{*2})= \frac{x_{0}^{2}}{2}((z^*+z)^2+1)= \frac{x_{0}^{2}}{2}(4Re(z)^2+1)

Drugi člen izrazimo z zvezo 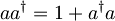aa^\dagger=1+a^\dagger a, tako da je v produktu anihilacijski operator pred kreacijskim.

Ker so koherentna stanja lastna stanja anihilacijskega operatorja jih lahko izrazimo iz anihilacijskega operatorja preko:

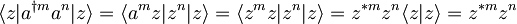
\langle z|a^{\dagger m}a^{n}|z\rangle = \langle a^m z|z^n|z\rangle = \langle z^m z|z^n|z \rangle =z^{*m}z^n\langle z|z \rangle = z^{*m}z^n


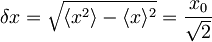
Nedoločenost lege je: \delta x= \sqrt{\langle x^2\rangle -\langle x\rangle^2}=\frac{x_{0}}{\sqrt{2}}


Nedoločenost gibalne količine

Na podoben način dobimo nedoločenost gibalne količine.

Operator gibalne količine 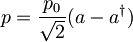p=\frac{p_{0}}{\sqrt{2}}(a-a^\dagger), kjer je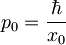 p_{0}=\frac{\hbar}{x_{0}}

Povprečna vrednost gibalne količine:

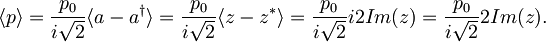
\langle p\rangle =\frac{p_{0}}{i \sqrt{2}} \langle a-a^\dagger \rangle=\frac{p_{0}}{i \sqrt{2}} \langle z-z^* \rangle= \frac{p_{0}}{i \sqrt{2}}i 2Im(z)=\frac{p_{0}}{i \sqrt{2}}2Im(z).

Povprečje kvadrata gibalne količine:

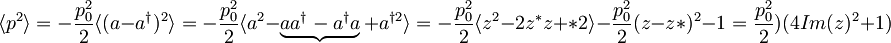
\langle p^2\rangle =-\frac{p_{0}^{2}}{2} \langle (a-a^\dagger)^2 \rangle= -\frac{p_{0}^{2}}{2}\langle a^2 - \underbrace{aa^\dagger-a^\dagger a}+a^{\dagger 2} \rangle= -\frac{p_{0}^{2}}{2}\langle z^2 - 2z^*z+{*2} \rangle -\frac{p_{0}^{2}}{2} (z-z*)^2-1 =\frac{p_{0}^{2}}{2})(4Im(z)^2+1)

Nedoločenost gibalne količine je: \delta p= \sqrt{\langle p^2\rangle -\langle p\rangle^2}=\frac{p_{0}}{\sqrt{2}}

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Koherentna_stanja_harmonskega_oscilatorja_I«