Heisenbergov princip nedoločenosti I

Iz Kvantna Mehanika I 2006 - 2007

Naloga

1. Izpelji Heisenbergov princip nedoločenosti za produkt nedoločenosti dveh opazljivk.
2. Poišči valovno funkcijo z minimalnim produktom nedoločenosti položaja delca in njegove gibalne količine.

Rešitev

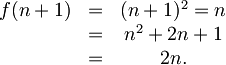
Ni mi uspelo razčleniti (Začasne mape za matematiko ne morem ustvariti ali pisati vanjo.): \langle \psi \: | \: \lbrace A', B' \rbrace \: \psi \rangle

Ni mi uspelo razčleniti (Začasne mape za matematiko ne morem ustvariti ali pisati vanjo.): \begin{matrix} \langle\psi\:|\:\lbrace A',B'\rbrace\:\psi\rangle & = & \langle\psi\:|\:(A'B'+B'A')\:\psi\rangle \\ & = & \langle A'\psi|B'\psi\rangle + \langle B'\psi|A'\psi\rangle = \\ 0 & = & \lambda^\ast\: \langle B'\psi|B'\psi\rangle + \lambda\: \langle B'\psi|B'\psi\rangle & = & \end{matrix}