Heisenbergov princip nedoločenosti I

Iz Kvantna Mehanika I 2006 - 2007

Vsebina

1 Naloga
2 Rešitev
- 2.1 Izpeljava Heisenbergovega načela
- 2.2 Valovni paket

[spremeni] Naloga

Izpelji Heisenbergov princip nedoločenosti za produkt nedoločenosti dveh opazljivk.
Poišči valovno funkcijo z minimalnim produktom nedoločenosti položaja delca in njegove gibalne količine.

[spremeni] Rešitev

[spremeni] Izpeljava Heisenbergovega načela

Pri izpeljavi Hesenbergovega načela za produkt nedoločenosti dveh splošnih količin A in B potrebujemo kar nekaj pomožnih računov. Povsod privzamemo normiranost valovne funkcije in dejstvo, da fizikalne količine v kvantni mehaniki nadomestijo ustrezni hermitski operatorji.

[spremeni] Hermitski operator

Hermitsko adjungiran operator k operatorju A mora izpolnjevati pogoj

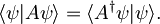
$\langle\psi|A\psi\rangle = \langle A^\dagger \psi|\psi\rangle .$

Če velja

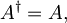
$A^\dagger = A ,$

pravimo, da je operator A sebi hermitsko adjungiran ali na kratko hermitski.

Izraz za pričakovane vrednosti hermitskega operatorja A

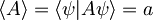
$\langle A\rangle = \langle\psi|A\psi\rangle = a$

lahko nekoliko predelamo, pri čemer upoštevamo še konjugirano komutativnost skalarnega produkta:

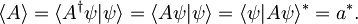
$\langle A\rangle = \langle A^\dagger\psi|\psi\rangle = \langle A\psi|\psi\rangle = \langle\psi|A\psi\rangle^\ast = a^\ast .$

Pričakovane vrednosti hermitskega operatorja so torej realne:

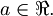
$a \in \Re .$

[spremeni] Antihermitski operator

Definirajmo sedaj še antihermitski operator:

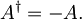
$A^\dagger = -A .$

Po enakem postopku kot zgoraj

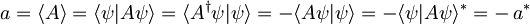
$a = \langle A\rangle = \langle\psi|A\psi\rangle = \langle A^\dagger\psi|\psi\rangle = -\langle A\psi|\psi\rangle = -\langle\psi|A\psi\rangle^\ast = -\,a^\ast$

izpeljemo

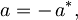
$a = -\,a^\ast ,$

torej so pričakovane vrednosti antihermitskega operatorja imaginarne

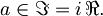
$a \in \Im = i \,\Re .$

[spremeni] Komutator

Komutator dveh operatorjev je po definiciji

$[A, B] = A B - B A .$

Z uporabo zveze za hermitiranje produkta

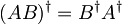
$(AB)^\dagger = B^\dagger A^\dagger$

ugotovimo,

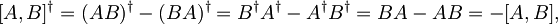
$\lbrack A,B\rbrack^\dagger = (AB)^\dagger - (BA)^\dagger = B^\dagger A^\dagger - A^\dagger B^\dagger = BA - AB = -\lbrack A,B \rbrack ,$

da je komutator antihermitski operator, njegove pričakovane vrednost so torej imaginarne.

[spremeni] Antikomutator

Definirajmo operator antikomutator:

${A, B} = A B + B A .$

Z njim ponovimo zgornji postopek

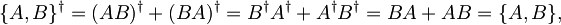
$\lbrace A,B \rbrace ^\dagger = (AB)^\dagger + (BA)^\dagger = B^\dagger A^\dagger + A^\dagger B^\dagger = BA + AB = \lbrace A,B \rbrace ,$

po katerem ugotovimo, da je antikomutator hermitski operator, torej ima realne pričakovane vrednosti.

[spremeni] Dekompozicija produkta

Vsak operator, definiran kot produkt dveh operatorjev A in B, očitno lahko razstavimo po pravilu:

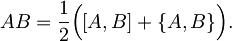
$AB = \frac{1}{2} \Bigl(\lbrack A,B \rbrack + \lbrace A,B \rbrace\Bigr) .$

[spremeni] Cauchy-Schwarzova neenakost

Za skalarni produkt velja pravilo

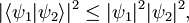
$| \langle \psi_1 | \psi_2 \rangle |^2 \leq |\psi_1|^2 |\psi_2|^2 ,$

kjer je seveda

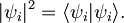
$|\psi_i|^2 = \langle \psi_i | \psi_i \rangle .$

Enakost velja le v primeru, ko sta vektorja (v našem primeru valovni funkciji) vzporedna:

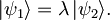
$|\psi_1 \rangle = \lambda \,|\psi_2 \rangle .$

[spremeni] Nedoločenost

Nedoločenost količine, ki jo predstavlja operator A, je definirana kot

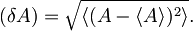
$(\delta A) = \sqrt{\langle (A - \langle A\rangle)^2 \rangle} .$

Če torej definiramo nov operator

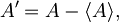
$A' = A - \langle A \rangle ,$

se zgornja enačba prepiše v

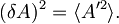
$(\delta A)^2 = \langle A'^2 \rangle .$

Ker je A hermitski, se lastnost očitno prenese tudi na A’ .

V komutatorju dveh tako transformiranih operatorjev

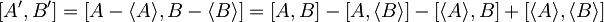
$\lbrack A',B' \rbrack = \lbrack A - \langle A \rangle, B - \langle B \rangle \rbrack = \lbrack A,B \rbrack - \lbrack A, \langle B \rangle \rbrack - \lbrack \langle A \rangle , B \rbrack + \lbrack \langle A \rangle , \langle B \rangle \rbrack$

je od nič različen le prvi člen, saj sta pričakovani vrednosti operatorjev A in B števili, ki komutirata tako s poljubnim operatorjem kot med seboj. Velja torej

$[A', B'] = [A, B].$

Za antikomutator ta lastnost seveda ne velja.

[spremeni] Heisenbergovo načelo

Z zgoraj definiranima hermitskima operatorjema sestavimo sedaj nova vektorja

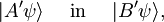
$|A' \psi \rangle \quad \mbox{ in } \quad |B' \psi \rangle ,$

ju vstavimo v Cauchy-Schwarzovo neenakost in preoblikujemo:

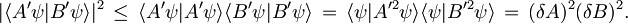
Na desni smo že dobili željeni produkt nedoločenosti, levega pa z upoštevanjem pravila o dekompoziciji ter lastnosti komutatorja A' in B' še nekoliko predelajmo:

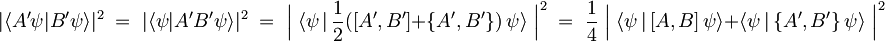$|\langle A'\psi |B'\psi \rangle|^2 \; = \; |\langle \psi |A'B'\psi \rangle|^2 \; = \; \Bigl\vert\;\langle\psi\,|\,\frac{1}{2} (\lbrack A',B' \rbrack + \lbrace A',B' \rbrace ) \, \psi \rangle \;\Bigl\vert ^2 \;=\; \frac{1}{4}\; \Bigl\vert \; \langle\psi\,| \,\lbrack A,B \rbrack \,\psi\rangle + \langle\psi\,|\,\lbrace A',B'\rbrace\,\psi\rangle\; \Bigl\vert ^2$ .

Ker je pričakovana vrednost komutatorja imaginarno, antikomutatorja pa realo število, je kvadrat absolutne vrednosti njune vsote kar enak vsoti kvadratov absolutnih vrednosti posameznih členov, pri čemer lahko absolutno vrednost pri antikomutatorju tudi izpustimo:

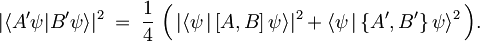
$|\langle A'\psi|B'\psi\rangle|^2 \;=\; \frac{1}{4} \; \Bigl(\,|\langle\psi\,| \,\lbrack A,B \rbrack \,\psi\rangle |^2 + \langle\psi\,|\,\lbrace A',B'\rbrace\,\psi\rangle^2\,\Bigr) .$

Če sedaj sestavimo levo in desno stran začetne enačbe,

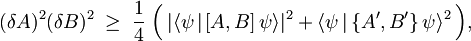
$(\delta A)^2 (\delta B)^2 \;\geq\; \frac{1}{4} \; \Bigl(\,|\langle\psi\,| \,\lbrack A,B \rbrack \,\psi\rangle |^2 + \langle\psi\,|\,\lbrace A',B'\rbrace\,\psi\rangle^2\,\Bigr) ,$

vidimo, da bo neenakost izpolnjena tudi brez drugega člena vsote, ki je vedno pozitivno realno število. Tako dobimo koncno obliko Heisenbergovega načela nedoločenosti

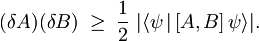
$(\delta A)(\delta B) \;\geq \; \frac{1}{2} \; |\langle\psi\,| \,\lbrack A,B \rbrack \,\psi\rangle| .$

[spremeni] Primer x in p

Preverimo dobljeno neenačbo na najpogosteje uporabljanem primeru – za nedoločenost lege in gibalne količine. Operatorja A in B nadomestimo z

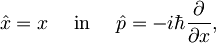
$\hat x = x \quad \mbox{ in } \quad \hat p = -i \hbar \frac{\partial}{\partial x} ,$

izračunamo njun komutator

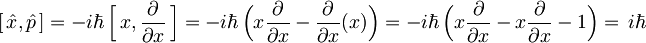
$\lbrack\,\hat x,\hat p\,\rbrack = -i\hbar\,\Bigl\lbrack\,x,\frac{\partial}{\partial x}\,\Bigr\rbrack = -i \hbar\,\Bigl(x \frac{\partial}{\partial x} - \frac{\partial}{\partial x}(x) \Bigr) = -i \hbar\,\Bigl(x \frac{\partial}{\partial x} - x \frac{\partial}{\partial x} - 1 \Bigr)= \, i \hbar$

in vstavimo v neenačbo:

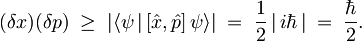
$(\delta x)(\delta p) \;\geq\; |\langle\psi\,|\,\lbrack \hat x,\hat p \rbrack \,\psi\rangle| \;=\; \frac{1}{2}\,|\,i\hbar\,| \;=\; \frac{\hbar}{2} .$

Res dobimo dobro poznano zvezo.

[spremeni] Valovni paket

Sedaj bi radi ugotovili, za kakšno valovno funkcijo bo produkt nedoločenosti lege in gibalne količine najmanjši, v splošnem torej

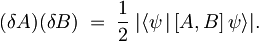
$(\delta A)(\delta B) \;=\; \frac{1}{2} \; |\langle\psi\,| \,\lbrack A,B \rbrack \,\psi\rangle| .$

Spomnimo se, da ima neenačaj dva prispevka:

Cauchy-Schwarzovo neenakost ter
neupoštevanje pričakovane vrednosti antikomutatorja.

Če želimo zapisati enakost, moramo torej zadostiti dvema zahtevama: vektorja morata biti vzporedna

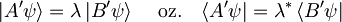
$|A'\psi\rangle = \lambda\,|B'\psi\rangle \quad \mbox{ oz.} \quad \langle A'\psi| = \lambda^\ast\,\langle B'\psi|$

(sorazmernostni faktor $λ$ je zaenkrat lahko še poljubno kompleksno število), pričakovna vrednost antikomutatorja pa enaka nič

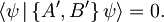
$\langle\psi\,|\,\lbrace A',B'\rbrace\,\psi\rangle = 0 .$

Ko združimo oba pogoja,

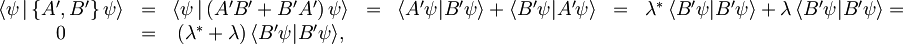
$\begin{matrix} \langle\psi\,|\,\lbrace A',B'\rbrace\,\psi\rangle & = & \langle\psi\,|\,(A'B'+B'A')\,\psi\rangle & = & \langle A'\psi|B'\psi\rangle + \langle B'\psi|A'\psi\rangle & = & \lambda^\ast\, \langle B'\psi|B'\psi\rangle + \lambda\, \langle B'\psi|B'\psi\rangle = \\ 0 & = & (\lambda^\ast + \lambda)\, \langle B'\psi|B'\psi\rangle ,& & & & \end{matrix}$

ugotovimo, da je $λ$ lahko le imaginarno število

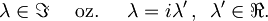
$\lambda \in \Im \quad \mbox{ oz. } \quad \lambda = i\lambda'\,,\,\,\, \lambda' \in \Re .$

V primeru lege in gibalne količine velja torej

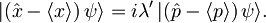
$|(\hat x-\langle x\rangle)\,\psi\rangle = i\lambda'\,|(\hat p-\langle p\rangle)\,\psi\rangle .$

Za izpeljavo iskane valovne funkcije moramo zdaj preiti iz vektorske v funkcijsko pisavo

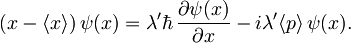
$(x-\langle x\rangle)\,\psi(x) = \lambda'\hbar\,\frac{\partial\psi(x)}{\partial x}-i\lambda'\langle p\rangle\,\psi(x) .$

Prepisana zveza predstavlja preprosto diferencialno enačbo za $ψ(x),$ katere rešitev je iskana valovna funkcija z najmanjšo nedoločenostjo. Pri reševanju le še ločimo spremenljivki

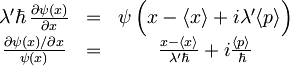
$\begin{matrix} \lambda'\hbar\,\frac{\partial\psi(x)}{\partial x} & = & \psi\, \Bigl(x-\langle x\rangle + i\lambda'\langle p\rangle \Bigr) \\ \frac{\partial \psi(x) / \partial x}{\psi(x)} & = & \frac{x-\langle x\rangle}{\lambda'\hbar}+i\frac{\langle p\rangle}{\hbar} \end{matrix}$

in integriramo na obeh straneh

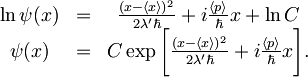
$\begin{matrix} \ln \psi(x) & = & \frac{(x-\langle x\rangle)^2}{2\lambda'\hbar}+i\frac{\langle p\rangle}{\hbar}x + \ln C \\ \psi(x) & = & C \exp\biggl\lbrack \frac{(x-\langle x\rangle)^2}{2\lambda'\hbar}+ i\frac{\langle p\rangle}{\hbar}x \biggr\rbrack. \end{matrix}$

Integracijsko konstanto določimo z normalizacijo valovne funkcije:

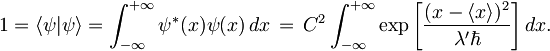
$1 = \langle\psi|\psi\rangle = \int_{-\infty}^{+\infty}\psi^\ast(x)\psi(x)\,d x \,=\, C^2 \int_{-\infty}^{+\infty} \exp\biggl\lbrack \frac{(x-\langle x\rangle)^2}{\lambda'\hbar}\biggr\rbrack\,d x .$

Dobljeni Gaussov integral je izvedljiv le za $λ'$ < 0. Po predelavi v brezdimenzijsko obliko za rešitev dobimo

$1 = C^2 \,\sqrt{\frac{-\lambda'\hbar}{2}} \,\sqrt{2\pi} \qquad \Rightarrow \qquad C = \sqrt[4]{\frac{1}{-\lambda'\hbar\pi}}$

(po korakih smo podobne integrale računali pri Fiziki II). Če konstante še preimenujemo v skladu s splošno sprejetimi oznakami, tako da je

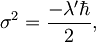
$\sigma^2 = \frac{-\lambda'\hbar}{2} ,$

dobimo standardni izraz za valovni paket

$\psi(x) = \frac{1}{\sqrt[4]{2\pi\sigma^2}} \exp\biggl\lbrack -\frac{(x-\langle x\rangle)^2}{4\sigma^2}+ i\frac{\langle p\rangle}{\hbar}x \biggr\rbrack ,$

ki predstavlja valovno funkcijo z najmanjšo nedoločenostjo kraja in gibalne količine, kot jo dopušča Hesenbergovo načelo.

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Heisenbergov_princip_nedolo%C4%8Denosti_I«