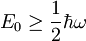Heisenbergov princip nedoločenosti II in komutatorske identitete

Iz Kvantna Mehanika I 2006 - 2007

Revision as of 20:49, 12 marec 2007 by Ruskicar (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Naloga

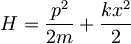S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja ( $H=\frac{p^2}{2m}+\frac{kx^2}{2}$ ).
Dokaži naslednje komutatorske identitete:
- Dokaži, da velja $[A, B n] = n B n - 1 [A, B]$ , če operatorja $A$ in $B$ zadoščata pogoju $[[A, B], B] = 0$ . Uporabi rezultat za izračun komutatorja $[A, f (B)]$ . Predpostavi, da se funkcija $f$ da razviti v Taylorjevo vrsto.
- Pokaži, da velja $e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}$ , če $[A, B]$ komutira z operatorjema $A$ in $B$ .
- Dokaži Baker-Hausdorffovo identiteto: $e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}$ .

Rešitev

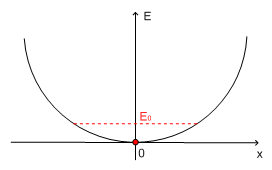
Energija osnovnega stanja harmonskega oscilatorja seveda ni enaka nič (kot bi to morda intuitivno pričakovali), saj bi s tem kršili Heisenbergov princip nedoločenosti, ki pravi, da delca ne moremo fiksirati točno na sredino potenciala in ga pustiti tam mirovati.

Da bi izračunali, kolikšna je minimalna dovoljena energija $E 0$ , da še ne kršimo Heisenbergovega principa nedoločenosti, moramo najprej izpisati operator polne energije harmonskega oscilatorja:

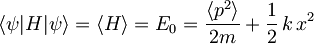
$\langle \psi | H | \psi \rangle = \langle H \rangle = E_0 = \frac{\langle p^2 \rangle}{2m} + \frac{1}{2}\,k\,x^2$

Ker je potencial simetričen okrog x = 0, je pričakovana vrednost koordinate x: 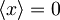$\langle x \rangle = 0$

Iz tega sledi, da je tudi pričakovana vrednost gibalne količine 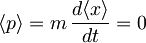$\langle p \rangle = m \, \frac{d\langle x \rangle}{dt} = 0$

Sedaj se spomnimo zvez 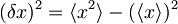$(\delta x)^2 = \langle x^2 \rangle - (\langle x \rangle)^2$ oziroma 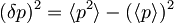$(\delta p)^2 = \langle p^2 \rangle - (\langle p \rangle)^2$ , iz katerih zaradi zgornjih pričakovanih vrednosti sledi:

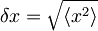
$\delta x = \sqrt{\langle x^2 \rangle}$

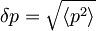
$\delta p =\sqrt{\langle p^2 \rangle}$

$E 0$ lahko sedaj zapišemo kot

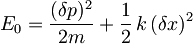
$E_0 = \frac{(\delta p)^2}{2m} + \frac{1}{2} \, k \, (\delta x)^2$

Ob upoštevanju Heisenbergovega principa nedoločenosti 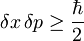$\delta x \, \delta p \geq \frac{\hbar}{2}$ pa sledi

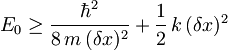
$E_0 \geq \frac{\hbar ^2}{8\,m\, (\delta x)^2} + \frac{1}{2} \, k \, (\delta x)^2$

Ker iščemo minimum energije, moramo torej odvod $E 0$ po $δ x$ izenačiti z 0:

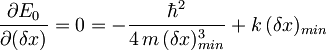
$\frac{\partial E_0}{\partial (\delta x)} = 0 = - \frac{\hbar ^2}{4\,m\, (\delta x)_{min}^3} + k \, (\delta x)_{min}$

kjer indeks min označuje minimalno nedoločenost lege.

Iz prejšnje enačbe dobimo $(\delta x)_{min} = \sqrt[4]{\frac{\hbar^2}{4\,k\,m}}$ , torej mora biti energija osnovnega stanja

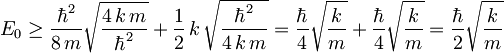
$E_0 \geq \frac{\hbar ^2}{8\,m} \sqrt{\frac{4\,k\,m}{\hbar^2}} + \frac{1}{2} \, k \, \sqrt{\frac{\hbar^2}{4\,k\,m}} = \frac{\hbar}{4} \sqrt{\frac{k}{m}} + \frac{\hbar}{4} \sqrt{\frac{k}{m}}= \frac{\hbar}{2} \sqrt{\frac{k}{m}}$

V zadnjem členu prepoznamo še frekvenco harmonskega oscilatorja 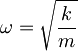$\omega = \sqrt{\frac{k}{m}}$ in končni rezultat za minimalno energijo osnovnega stanja harmonskega oscilatorja je

$E_0 \geq \frac{1}{2} \hbar \omega$

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Heisenbergov_princip_nedolo%C4%8Denosti_II_in_komutatorske_identitete«