Heisenbergov princip nedoločenosti II in komutatorske identitete
Iz Kvantna Mehanika I 2006 - 2007
[spremeni] Naloga
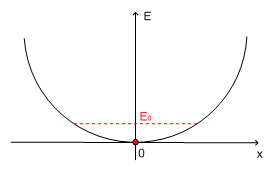
- S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (
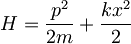 ).
).
- Dokaži naslednje komutatorske identitete:
- Dokaži, da velja [A,Bn] = nBn − 1[A,B], če operatorja A in B zadoščata pogoju [[A,B],B] = 0. Uporabi rezultat za izračun komutatorja [A,f(B)]. Predpostavi, da se funkcija f da razviti v Taylorjevo vrsto.
- Pokaži, da velja
![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png) , če [A,B] komutira z operatorjema A in B.
, če [A,B] komutira z operatorjema A in B.
- Dokaži Baker-Hausdorffovo identiteto:
![e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}](/wiki/images/math/6/9/5/695bedf4d6987cfb532bb2dd921e9629.png) .
.
[spremeni] Rešitev
1. del:
Energija osnovnega stanja harmonskega oscilatorja seveda ni enaka nič (kot bi to morda intuitivno pričakovali), saj bi s tem kršili Heisenbergov princip nedoločenosti, ki pravi, da delca ne moremo fiksirati točno na sredino potenciala in ga pustiti tam mirovati.
Da bi izračunali, kolikšna je minimalna dovoljena energija 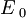 , da še ne kršimo Heisenbergovega principa nedoločenosti, moramo najprej izpisati operator polne energije harmonskega oscilatorja:
, da še ne kršimo Heisenbergovega principa nedoločenosti, moramo najprej izpisati operator polne energije harmonskega oscilatorja:
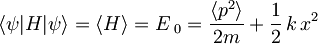
Ker je potencial simetričen okrog x = 0, je pričakovana vrednost koordinate x:
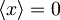 .
.
Iz tega sledi, da je tudi pričakovana vrednost gibalne količine
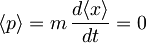 .
.
Sedaj se spomnimo zvez
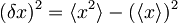
oziroma
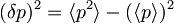 ,
,
iz katerih zaradi zgornjih pričakovanih vrednosti sledi:
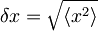 ,
,
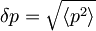 .
.
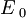 lahko sedaj zapišemo kot
lahko sedaj zapišemo kot
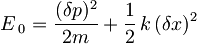 .
.
Ob upoštevanju Heisenbergovega principa nedoločenosti 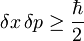 pa sledi
pa sledi
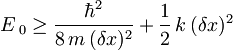 .
.
Ker iščemo minimum energije, moramo torej odvod 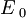 po
po 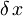 izenačiti z 0:
izenačiti z 0:
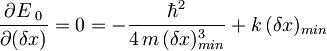 ,
,
kjer indeks min označuje minimalno nedoločenost lege.
Iz prejšnje enačbe dobimo
![(\delta x)_{min} = \sqrt[4]{\frac{\hbar^2}{4\,k\,m}}](/wiki/images/math/4/3/6/4368365787d43f893b7319b7a9e0bc7c.png) ,
,
torej mora biti energija osnovnega stanja
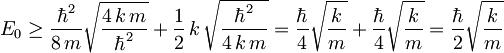 .
.
V zadnjem členu prepoznamo še frekvenco harmonskega oscilatorja
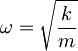
in končni rezultat za minimalno energijo osnovnega stanja harmonskega oscilatorja je
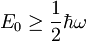 .
.
2. del:
a) Dokazati hočemo, da velja
![[A,B^n]=n\, B^{n-1}\,[A,B]](/wiki/images/math/6/5/0/650492541930eb3e3cd763b9a5ab6ada.png) ,
,
če operatorja A in B zadoščata pogoju ![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png) . Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n:
. Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n:
![n = 1: \quad [A,B^1] = [A,B]](/wiki/images/math/7/4/b/74bf35148f039f67ae64cc64adcd3455.png) .
.
![n > 1: \quad [A, B^n] = [A, B \, B^{n-1}] = B [A,B^{n-1}] + [A,B] B^{n-1} =](/wiki/images/math/d/d/d/dddf58e808935af6a7486464c1054e81.png)
![B\,(n-1)\, B^{n-2}\, [A,B] + [A,B]\, B^{n-1} =](/wiki/images/math/0/9/b/09b22a0bee3c3b36499645a28add3339.png)
![B^{n-1}\, [A,B]\, (n-1 + 1) = n\, B^{n-1}\, [A,B]](/wiki/images/math/f/0/1/f011af8882f713f1665f365f56a239df.png) .
.
V prvi vrstici smo uporabili lastnost komutatorja
![[A,BC] = B\,[A,C] + [A,B]\,C](/wiki/images/math/b/e/6/be623ce951eff27e9604590ac0bdb024.png) ,
,
iz prve v v drugo vrstico pa smo uporabili trditev, ki jo dokazujemo:
![[A,B^n]=n\, B^{n-1}\,[A,B]](/wiki/images/math/6/5/0/650492541930eb3e3cd763b9a5ab6ada.png) .
.
Nazadnje smo uporabili še pogoj, da je
![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png)
oz. da operator 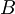 komutira s komutatorjem
komutira s komutatorjem ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) .
.
Ker zadnja enačba velja za vsak n > 1 in ker velja za n=1, je torej dokaz zaključen.
S pomočjo te enačbe bomo sedaj izračunali komutator
![[A,\, f(B)]](/wiki/images/math/2/a/0/2a0ec4c99e849b7de26273db00ed80b8.png) ,
,
kjer predpostavimo, da se funkcija 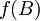 da razviti v Taylorjevo vrsto, torej:
da razviti v Taylorjevo vrsto, torej:
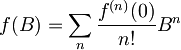 .
.
![[A,\, f(B)] = [A, \sum_n \frac{f^{(n)}(0)}{n!}B^n ] = \sum_n \frac{f^{(n)}(0)}{n!} [A, B^n] = \sum_n \frac{f^{(n)}(0)}{n!} \, n \, B^{n-1}\, [A, B]](/wiki/images/math/b/2/7/b270ddbddcb0999d36219ce028b8d0a9.png) .
.
Vsoto lahko nesemo ven iz komutatorja, ker veljata zvezi
![[A, B+C] = [A,B] \, + \, [A,C]](/wiki/images/math/3/6/7/3679a3c4eae96b1fe9abeed38564782f.png)
ter
![[A, \lambda B] = \lambda \, [A,B]](/wiki/images/math/9/2/8/928e3bb757ff68756ec97a0a9d8ad16d.png) .
.
V zadnjem izrazu
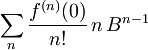
pa prepoznamo ravno odvod 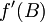 . Rezultat je torej
. Rezultat je torej
![[A,\, f(B)] = f'(B)\,[A,B]](/wiki/images/math/1/1/7/11758588564e29603d3260f5fadff7f5.png) .
.
b) Naša naslednja naloga je bila pokazati, da velja
![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png) ,
,
če ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) komutira z operatorjema
komutira z operatorjema 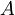 in
in 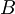 , torej
, torej
![[[A,B],\,A]=0](/wiki/images/math/8/9/9/899c97e1454e46f9bb4f4eb4b422062c.png)
in
![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png) .
.
Naloge se lotimo tako, da vpeljemo funkcijo
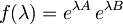
in izračunamo odvod te funkcije:
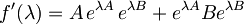 .
.
Tu moramo seveda paziti, da operatorja 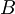 ne nesemo pred eksponent, saj ni nujno, da komutira z
ne nesemo pred eksponent, saj ni nujno, da komutira z 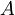 . Zato si pomagamo z enačbo:
. Zato si pomagamo z enačbo:
![[e^{\lambda A}, B] = - [B, e^{\lambda A}] = - \lambda \, e^{\lambda A} [B,A] = \lambda\, e^{\lambda A} [A,B]](/wiki/images/math/b/1/3/b1339f207a8c0a88a1243cb3fcc2ce4e.png) .
.
Tu smo uporabili rezultat iz prejšnjega dela 2. naloge,
![[B,\, f(A)] = f'(A)\,[B,A]](/wiki/images/math/2/1/5/2154e03a9939906e9ed27a0470a8bef5.png) .
.
Seveda pa lahko že prvi komutator takoj na začetku zapišemo kot
![[e^{\lambda A}, B] = e^{\lambda A}\,B - B\,e^{\lambda A}](/wiki/images/math/9/d/4/9d48b982d179ac42b161805b30838629.png) .
.
Če to dvoje potem izenačimo, lahko izrazimo
![e^{\lambda A}\,B =B\,e^{\lambda A} + \lambda\, e^{\lambda A} [A,B]](/wiki/images/math/a/f/4/af46b492a8dbb06555eeae6e92ad719f.png) .
.
Sedaj se vrnemo nazaj na 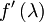 , ki ga lahko z novimi izrazi zapišemo kot
, ki ga lahko z novimi izrazi zapišemo kot
![f'(\lambda ) = A\,e^{\lambda A} \, e^{\lambda B} + (B\, e^{\lambda A} + \lambda e^{\lambda A} [A,B]) e^{\lambda B} = (A + B + \lambda [A,B]) e^{\lambda A} \, e^{\lambda B} = (A + B + \lambda [A,B]) f (\lambda)](/wiki/images/math/3/8/8/388d39934af2225353821dfaa246350c.png)
Tu pa komutator ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) lahko nesem pred eksponent, saj se da eksponent
lahko nesem pred eksponent, saj se da eksponent 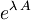 zapisati v Taylorjevo vrsto, v kateri nastopajo potence operatorja
zapisati v Taylorjevo vrsto, v kateri nastopajo potence operatorja 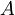 , s katerim po predpostavki komutator
, s katerim po predpostavki komutator ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) komutira.
komutira.
Dobimo diferencialno enačbo prvega reda, ki ima rešitev
![\ln( f(\lambda)) = (A+B)\lambda + [A,B] \frac{\lambda ^2}{2} + \ln C](/wiki/images/math/2/a/5/2a5d4d86d03832a86af08def80dcfe6c.png)
oziroma
![f(\lambda) = C e^{(A+B)\lambda + [A,B] \frac{\lambda ^2}{2}}](/wiki/images/math/f/8/6/f86a7ce5322d68b4129cb18bab6896ae.png) .
.
Konstanto C določimo, če postavimo
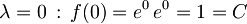 .
.
Če postavimo za 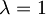 pa dobimo željen rezultat:
pa dobimo željen rezultat:
![f(1) = e^{(A+B)}e^{[A,B] \frac{1}{2}} = e^A\,e^B](/wiki/images/math/6/0/1/6012478b583ed330653aa29060cda282.png) .
.
Tukaj smo zopet uporabili dejstvo, da se da eksponentno funkcijo razviti v Taylorjevo vrsto, kjer se da vsoto po dveh indeksih pretvoriti na produkt dveh vsot. Zato lahko eksponent vsote pišemo kot produkt dveh eksponentov. Zadnjo enačbo se da zapisati tudi kot
![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png) ,
,
kar smo pravzaprav hoteli pokazati.
c) Zadnja naloga je od nas zahtevala, da dokažemo Baker-Hausdorffovo identiteto:
![e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}](/wiki/images/math/6/9/5/695bedf4d6987cfb532bb2dd921e9629.png)
Tudi pri tej nalogi vpeljemo funkcijo
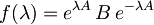 ,
,
za katero predpostavimo, da se jo da razviti v Taylorjevo vrsto:
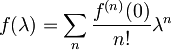 .
.
Če izračunamo prvi odvod te funkcije, dobimo
![f'(\lambda) = A e^{\lambda A}\,B\,e^{-\lambda A} - e^{\lambda A}\,B\,A\,e^{-\lambda A} = e^{\lambda A}\,[A,B]\,e^{-\lambda A}](/wiki/images/math/0/8/f/08f3e919d3a0b460022d3ee772f0408e.png) .
.
Operator 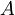 seveda komutira sam s sabo, zato ga lahko v prvem členu nesemo za eksponent.
seveda komutira sam s sabo, zato ga lahko v prvem členu nesemo za eksponent.
Podobno je drugim ter tretjim odvodom funkcije:
![f''(\lambda) = e^{\lambda A}\,[A,[A,B]]\,e^{-\lambda A}](/wiki/images/math/2/3/d/23d176346ebaff7887a879a4b02bf0aa.png)
![f'''(\lambda) = e^{\lambda A}\,[A,[A,[A,B]]]\,e^{-\lambda A}](/wiki/images/math/6/f/9/6f9e8d10e9907e54fa274346b2c035bb.png) .
.
Ko vse to zložimo v Taylorjevo vrsto funkcije, pri čemer upoštevamo, da so odvodi v Taylorjevem razvoju izraženi v točki 0, dobimo
![f(\lambda) = e^{\lambda A}\,B\,e^{-\lambda A} = B + [A,B] \lambda + [A,[A,B]] \frac{\lambda ^2}{2!} + {\ldots}](/wiki/images/math/3/b/6/3b6ba7b7855818c526a14207d6d7fc31.png) .
.
To pa je v primeru 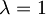 ravno Baker - Hausdorffova identiteta.
ravno Baker - Hausdorffova identiteta.