Heisenbergov princip nedoločenosti II in komutatorske identitete

(Primerjava redakcij)

Redakcija: 18:50, 5 marec 2007

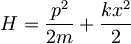S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja ( $H=\frac{p^2}{2m}+\frac{kx^2}{2}$ ).
Dokaži naslednje komutatorske identitete:
- Dokaži, da velja $[A, B n] = n B n - 1 [A, B]$ , če operatorja $A$ in $B$ zadoščata pogoju $[[A, B], B] = 0$ . Uporabi rezultat za izračun komutatorja $[A, f (B)]$ . Predpostavi, da se funkcija $f$ da razviti v Taylorjevo vrsto.
- Pokaži, da velja $e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}$ , če $[A, B]$ komutira z operatorjema $A$ in $B$ .
- Dokaži Baker-Hausdorffovo identiteto: $e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}$ .

+== Naloga ==
 # S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (<math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>).
 # Dokaži naslednje komutatorske identitete:
 #* Pokaži, da velja <math>e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}</math>, če <math>[A,B]</math> komutira z operatorjema <math>A</math> in <math>B</math>.
 #* Dokaži Baker-Hausdorffovo identiteto: <math>e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}</math>.
+== Rešitev ==