1D vodikov atom
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 21:05, 9 september 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == Elektron se giblje vzdolž tanke cevke, ki je pravokotna na prevodno ploščo. Na površini plošče se nabere pozitiven naboj, zato elektron čuti privlačno silo, ki je tak...) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (10:50, 24 september 2007) (spremeni) (undo) WikiSysop (Pogovor | prispevki) |
||
| Vrstica 18: | Vrstica 18: | ||
| # Ploščo ob času <math>t=0</math> enakomerno nabijemo, tako da je površinska gostota naboja <math>\sigma</math>. Naboj nato počasi odteka s plošče, <math>\sigma(t)=\sigma e^{-t/\tau}</math>. Kolikšna je verjetnost, da je po dolgem času elektron v prvem vzbujenem stanju. Računaj v prvem redu perturbacije. | # Ploščo ob času <math>t=0</math> enakomerno nabijemo, tako da je površinska gostota naboja <math>\sigma</math>. Naboj nato počasi odteka s plošče, <math>\sigma(t)=\sigma e^{-t/\tau}</math>. Kolikšna je verjetnost, da je po dolgem času elektron v prvem vzbujenem stanju. Računaj v prvem redu perturbacije. | ||
| - | == Rešitev == | + | == [[Media:Vavpotic.pdf|Rešitev]] == |
Trenutna redakcija
[spremeni] Naloga
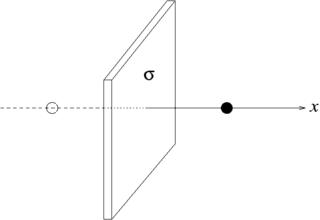
Elektron se giblje vzdolž tanke cevke, ki je pravokotna na prevodno ploščo. Na površini plošče se nabere pozitiven naboj, zato elektron čuti privlačno silo, ki je taka, kot da bi na nasprotni strani plošče stala zrcalna slika elektrona z nasprotnim nabojem.
Potencial, ki ga čuti elektron, je
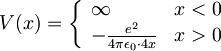 .
.
- Določi valovni funkciji in energiji osnovnega in prvega vzbujenega stanja. Namig: Uporabi rešitve za vodikov atom.
- Izračunaj produkt nedoločenosti položaja in gibalne količine elektrona v osnovnem stanju sistema.
- Ploščo ob času t = 0 enakomerno nabijemo, tako da je površinska gostota naboja σ. Naboj nato počasi odteka s plošče, σ(t) = σe − t / τ. Kolikšna je verjetnost, da je po dolgem času elektron v prvem vzbujenem stanju. Računaj v prvem redu perturbacije.