Časovno odvisna perturbacija III
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 17:27, 1 junij 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == Vodikov atom v osnovnem stanju je v časovno odvisnem potencialu <math>V(\mathbf{r},t)=V_0\cos{(kz-\omega t)}</math>. V prvem redu perturbacije izračunaj porazdelitev emi...) ← Pojdi na prejšnje urejanje |
Redakcija: 17:28, 1 junij 2007 (spremeni) (undo) WikiSysop (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 9: | Vrstica 9: | ||
| <math>\psi(\mathbf{r})=\frac{1}{L^{3/2}}\exp{\frac{i\mathbf{p}\cdot\mathbf{r}}{\hbar}}</math>. | <math>\psi(\mathbf{r})=\frac{1}{L^{3/2}}\exp{\frac{i\mathbf{p}\cdot\mathbf{r}}{\hbar}}</math>. | ||
| - | Na koncu računa lahko narediš limito <math>L\rightarrow\infty</math>. | + | <math>L</math> naj bo zelo velik, na koncu računa lahko narediš limito <math>L\rightarrow\infty</math>. |
| == Rešitev == | == Rešitev == | ||
Redakcija: 17:28, 1 junij 2007
Naloga
Vodikov atom v osnovnem stanju je v časovno odvisnem potencialu
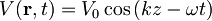 .
.
V prvem redu perturbacije izračunaj porazdelitev emitiranih elektronov po smeri in velikosti gibalne količine p. Za končno valovno funkcijo elektrona lahko vzameš ravne valove v potencialni jami s stranico L:
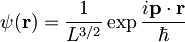 .
.
L naj bo zelo velik, na koncu računa lahko narediš limito 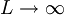 .
.