Heisenbergov princip nedoločenosti II in komutatorske identitete
Iz Kvantna Mehanika I 2006 - 2007
| Redakcija: 21:11, 12 marec 2007 (spremeni) Ruskicar (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Redakcija: 22:13, 12 marec 2007 (spremeni) (undo) Ruskicar (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 9: | Vrstica 9: | ||
| == Rešitev == | == Rešitev == | ||
| - | 1. Energija osnovnega stanja harmonskega oscilatorja seveda ni enaka nič (kot bi to morda intuitivno pričakovali), saj bi s tem kršili Heisenbergov princip nedoločenosti, ki pravi, da delca ne moremo fiksirati točno na sredino potenciala in ga pustiti tam mirovati. | + | '''1. del:''' |
| + | |||
| + | Energija osnovnega stanja harmonskega oscilatorja seveda ni enaka nič (kot bi to morda intuitivno pričakovali), saj bi s tem kršili Heisenbergov princip nedoločenosti, ki pravi, da delca ne moremo fiksirati točno na sredino potenciala in ga pustiti tam mirovati. | ||
| [[Slika:Skica-ho.gif]] | [[Slika:Skica-ho.gif]] | ||
| Vrstica 51: | Vrstica 53: | ||
| ---- | ---- | ||
| - | 2. Dokazati hočemo, da velja <math>[A,B^n]=n\, B^{n-1}\,[A,B]</math>, če operatorja A in B zadoščata pogoju <math>[[A,B],\,B]=0</math>. Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n: | + | '''2. del:''' |
| + | |||
| + | ''a)'' Dokazati hočemo, da velja <math>[A,B^n]=n\, B^{n-1}\,[A,B]</math>, če operatorja A in B zadoščata pogoju <math>[[A,B],\,B]=0</math>. Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n: | ||
| <math>n = 1: \quad [A,B^1] = [A,B] </math> | <math>n = 1: \quad [A,B^1] = [A,B] </math> | ||
| - | <math>n \geq 1: \quad [A, B^n] = [A, B\, B^{n-1}]= B[A,B^{n-1}] + [A,B]\,B^{n-1} = B\,(n-1)\,B^{n-2}\,[A,B] + [A,B]\,B^{n-1} = B^{n-1}\,[A,B] (n-1 + 1) = n\,B^{n-1}\,[A,B]</math> | + | <math>n > 1: \quad [A, B^n] = [A, B\, B^{n-1}]= B[A,B^{n-1}] + [A,B]\,B^{n-1} = </math> |
| + | |||
| + | <math>= B\,(n-1)\,B^{n-2}\,[A,B] + [A,B]\,B^{n-1} = </math> | ||
| + | |||
| + | <math> = B^{n-1}\,[A,B] (n-1 + 1) = n\,B^{n-1}\,[A,B]</math> | ||
| + | |||
| + | V prvi vrstici smo uporabili lastnost komutatorja <math> [A,BC] = B\,[A,C] + [A,B]\,C </math>, v drugi vrstici smo uporabili trditev <math>[A,B^n]=n\, B^{n-1}\,[A,B]</math>, ki jo dokazujemo, nazadnje pa smo uporabili še pogoj, da je <math>[[A,B],\,B]=0</math> oz. da operator <math>B\,</math> komutira s komutatorjem <math>[A,\,B]</math>. | ||
| + | |||
| + | Ker torej zadnja enačba velja za vsak n > 1 in ker velja za n=1, je torej dokaz zaključen. S pomočjo te enačbe bomo sedaj izračunali komutator <math>[A,\, f(B)]</math>, kjer predpostavimo, da se funkcija <math>f(B)\,</math> da razviti v Taylorjevo vrsto, torej: | ||
| + | |||
| + | <math>f(B)=\sum_n \frac{f^{(n)}(0)}{n!}B^n</math> | ||
| + | |||
| + | <math>[A,\, f(B)] = [A, \sum_n \frac{f^{(n)}(0)}{n!}B^n ] = \sum_n \frac{f^{(n)}(0)}{n!} [A, B^n] = \sum_n \frac{f^{(n)}(0)}{n!} \, n \, B^{n-1}\, [A, B] </math> | ||
| + | |||
| + | Vsoto lahko nesemo ven iz komutatorja, ker veljata zvezi <math>[A, B+C] = [A,B] \, + \, [A,C]</math> ter <math>[A, \lambda B] = \lambda \, [A,B]</math> | ||
| + | |||
| + | V zadnjem izrazu <math>\sum_n \frac{f^{(n)}(0)}{n!} \, n \, B^{n-1}</math> pa prepoznamo ravno odvod <math>f'(B)\,</math>. Rezultat je torej | ||
| + | |||
| + | <math>[A,\, f(B)] = f'(B)\,[A,B] </math> | ||
| + | |||
| + | |||
| + | ''b)'' Naša naslednja naloga je bila pokazati, da velja <math>e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}</math>, če <math>[A,\,B]</math> komutira z operatorjema <math>A\,</math> in <math>B\,</math>, torej <math>[[A,B],\,A]=0</math> in <math> [[A,B],\,B]=0 </math>. | ||
| + | |||
| + | Naloge se lotimo tako, da vpeljemo funkcijo <math>f(\lambda ) = e^{\lambda A} \, e^{\lambda B}</math> in izračunamo odvod te funkcije: | ||
| + | |||
| + | <math>f'(\lambda ) = A\,e^{\lambda A} \, e^{\lambda B} + e^{\lambda A} B e^{\lambda B}</math> | ||
| + | |||
| + | Tu moramo seveda paziti, da operatorja <math>B\,</math> ne nesemo pred eksponent, saj ni nujno, da komutira z <math>A\,</math>. Zato si pomagamo z enačbo: | ||
| + | |||
| + | <math>[e^{\lambda A}, B] = - [B, e^{\lambda A}] = - \lambda \, e^{\lambda A} [B,A] = \lambda\, e^{\lambda A} [A,B]</math> | ||
| + | |||
| + | Tu smo uporabili rezultat iz prejšnjega dela 2. naloge, <math>[B,\, f(A)] = f'(A)\,[B,A] </math>. Seveda pa lahko že prvi komutator zapišemo kot <math>[e^{\lambda A}, B] = e^{\lambda A}\,B - B\,e^{\lambda A}</math>. Če to dvoje potem izenačimo, lahko izrazimo | ||
| + | |||
| + | <math>e^{\lambda A}\,B =B\,e^{\lambda A} + \lambda\, e^{\lambda A} [A,B] </math> | ||
| + | |||
| + | Sedaj se vrnemo nazaj na <math>f'\,(\lambda)</math>, ki ga lahko z novimi izrazi zapišemo kot | ||
| + | |||
| + | <math>f'(\lambda ) = A\,e^{\lambda A} \, e^{\lambda B} + (B\, e^{\lambda A} + \lambda e^{\lambda A} [A,B]) e^{\lambda B} = (A + B + \lambda [A,B]) e^{\lambda A} \, e^{\lambda B} = (A + B + \lambda [A,B]) f (\lambda) </math> | ||
| + | |||
| + | Tu pa komutator <math>[A,\,B]</math> lahko nesem pred eksponent, saj se da eksponent <math> e^{\lambda \, A} </math> zapisati v Taylorjevo vrsto, v kateri nastopajo potence operatorja <math>A\,</math>, s katerim po predpostavki komutator <math>[A,\,B]</math> komutira. | ||
| + | |||
| + | Dobimo diferencialno enačbo prvega reda, ki ima rešitev | ||
| + | |||
| + | <math>\ln( f(\lambda)) = (A+B)\lambda + [A,B] \frac{\lambda ^2}{2} + \ln C</math> | ||
| + | |||
| + | <math>f(\lambda) = C e^{(A+B)\lambda + [A,B] \frac{\lambda ^2}{2}}</math> | ||
| + | |||
| + | Konstanto C določimo, če postavimo <math>\lambda = 0 \,:\, f(0) = e^0\,e^0 = 1 = C</math> | ||
| + | |||
| + | Če postavimo za <math>\lambda = 1\,</math> pa dobimo željen rezultat: | ||
| + | |||
| + | <math>f(1) = e^{(A+B)}e^{[A,B] \frac{1}{2}} = e^A\,e^B</math> | ||
| + | |||
| + | Tukaj smo zopet uporabili dejstvo, da se da eksponentno funkcijo razviti v Taylorjevo vrsto, kjer se da vsoto po dveh indeksih pretvoriti na produkt dveh vsot. Zato lahko eksponent vsote pišemo kot produkt dveh eksponentov. Zadnjo enačbo se da zapisati tudi kot | ||
| + | |||
| + | <math>e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}</math> | ||
| + | |||
| + | kar smo pravzaprav hoteli pokazati. | ||
| - | Najprej smo uporabili lastnost komutatorja <math> [A,BC] = B\,[A,C] + [A,B]\,C </math>,potem smo uporabili trditev <math>[A,B^n]=n\, B^{n-1}\,[A,B]</math>, ki jo dokazujemo, nazadnje pa smo uporabili še pogoj, da je <math>[[A,B],\,B]=0</math> oz. da operator B komutira s komutatorjem [A,B]. | + | ''c)'' Zadnja naloga je od nas zahtevala, da dokažemo Baker-Hausdorffovo identiteto: <math>e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}</math>. |
Redakcija: 22:13, 12 marec 2007
Naloga
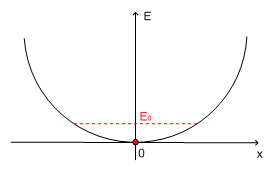
- S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (
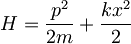 ).
).
- Dokaži naslednje komutatorske identitete:
- Dokaži, da velja [A,Bn] = nBn − 1[A,B], če operatorja A in B zadoščata pogoju [[A,B],B] = 0. Uporabi rezultat za izračun komutatorja [A,f(B)]. Predpostavi, da se funkcija f da razviti v Taylorjevo vrsto.
- Pokaži, da velja
![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png) , če [A,B] komutira z operatorjema A in B.
, če [A,B] komutira z operatorjema A in B.
- Dokaži Baker-Hausdorffovo identiteto:
![e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}](/wiki/images/math/6/9/5/695bedf4d6987cfb532bb2dd921e9629.png) .
.
Rešitev
1. del:
Energija osnovnega stanja harmonskega oscilatorja seveda ni enaka nič (kot bi to morda intuitivno pričakovali), saj bi s tem kršili Heisenbergov princip nedoločenosti, ki pravi, da delca ne moremo fiksirati točno na sredino potenciala in ga pustiti tam mirovati.
Da bi izračunali, kolikšna je minimalna dovoljena energija 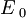 , da še ne kršimo Heisenbergovega principa nedoločenosti, moramo najprej izpisati operator polne energije harmonskega oscilatorja:
, da še ne kršimo Heisenbergovega principa nedoločenosti, moramo najprej izpisati operator polne energije harmonskega oscilatorja:
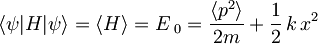
Ker je potencial simetričen okrog x = 0, je pričakovana vrednost koordinate x: 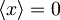
Iz tega sledi, da je tudi pričakovana vrednost gibalne količine 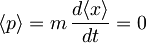
Sedaj se spomnimo zvez 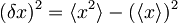 oziroma
oziroma 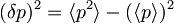 , iz katerih zaradi zgornjih pričakovanih vrednosti sledi:
, iz katerih zaradi zgornjih pričakovanih vrednosti sledi:
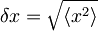
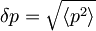
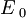 lahko sedaj zapišemo kot
lahko sedaj zapišemo kot
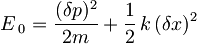
Ob upoštevanju Heisenbergovega principa nedoločenosti 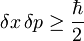 pa sledi
pa sledi
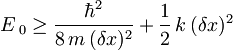
Ker iščemo minimum energije, moramo torej odvod 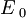 po
po 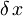 izenačiti z 0:
izenačiti z 0:
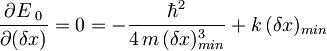
kjer indeks min označuje minimalno nedoločenost lege.
Iz prejšnje enačbe dobimo ![(\delta x)_{min} = \sqrt[4]{\frac{\hbar^2}{4\,k\,m}}](/wiki/images/math/4/3/6/4368365787d43f893b7319b7a9e0bc7c.png) , torej mora biti energija osnovnega stanja
, torej mora biti energija osnovnega stanja
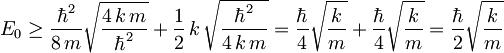
V zadnjem členu prepoznamo še frekvenco harmonskega oscilatorja 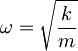 in končni rezultat za minimalno energijo osnovnega stanja harmonskega oscilatorja je
in končni rezultat za minimalno energijo osnovnega stanja harmonskega oscilatorja je
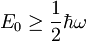
2. del:
a) Dokazati hočemo, da velja ![[A,B^n]=n\, B^{n-1}\,[A,B]](/wiki/images/math/6/5/0/650492541930eb3e3cd763b9a5ab6ada.png) , če operatorja A in B zadoščata pogoju
, če operatorja A in B zadoščata pogoju ![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png) . Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n:
. Dokaza se lotimo s principom popolne indukcije. Najprej preverimo, če izraz velja za n=1, potem pa predpostavimo, da velja za n-1 in iz tega pokažemo, da velja tudi za n:
![n = 1: \quad [A,B^1] = [A,B]](/wiki/images/math/7/4/b/74bf35148f039f67ae64cc64adcd3455.png)
![n > 1: \quad [A, B^n] = [A, B\, B^{n-1}]= B[A,B^{n-1}] + [A,B]\,B^{n-1} =](/wiki/images/math/9/9/1/9918c4150ac6f3ef40691603b4e14ce2.png)
![= B\,(n-1)\,B^{n-2}\,[A,B] + [A,B]\,B^{n-1} =](/wiki/images/math/d/d/4/dd4ee2317c66016f2fc2ea85090052f0.png)
![= B^{n-1}\,[A,B] (n-1 + 1) = n\,B^{n-1}\,[A,B]](/wiki/images/math/8/8/a/88a16055d1ef62bd2ea129d42432c78f.png)
V prvi vrstici smo uporabili lastnost komutatorja ![[A,BC] = B\,[A,C] + [A,B]\,C](/wiki/images/math/b/e/6/be623ce951eff27e9604590ac0bdb024.png) , v drugi vrstici smo uporabili trditev
, v drugi vrstici smo uporabili trditev ![[A,B^n]=n\, B^{n-1}\,[A,B]](/wiki/images/math/6/5/0/650492541930eb3e3cd763b9a5ab6ada.png) , ki jo dokazujemo, nazadnje pa smo uporabili še pogoj, da je
, ki jo dokazujemo, nazadnje pa smo uporabili še pogoj, da je ![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png) oz. da operator
oz. da operator 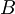 komutira s komutatorjem
komutira s komutatorjem ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) .
.
Ker torej zadnja enačba velja za vsak n > 1 in ker velja za n=1, je torej dokaz zaključen. S pomočjo te enačbe bomo sedaj izračunali komutator ![[A,\, f(B)]](/wiki/images/math/2/a/0/2a0ec4c99e849b7de26273db00ed80b8.png) , kjer predpostavimo, da se funkcija
, kjer predpostavimo, da se funkcija 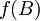 da razviti v Taylorjevo vrsto, torej:
da razviti v Taylorjevo vrsto, torej:
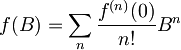
![[A,\, f(B)] = [A, \sum_n \frac{f^{(n)}(0)}{n!}B^n ] = \sum_n \frac{f^{(n)}(0)}{n!} [A, B^n] = \sum_n \frac{f^{(n)}(0)}{n!} \, n \, B^{n-1}\, [A, B]](/wiki/images/math/b/2/7/b270ddbddcb0999d36219ce028b8d0a9.png)
Vsoto lahko nesemo ven iz komutatorja, ker veljata zvezi ![[A, B+C] = [A,B] \, + \, [A,C]](/wiki/images/math/3/6/7/3679a3c4eae96b1fe9abeed38564782f.png) ter
ter ![[A, \lambda B] = \lambda \, [A,B]](/wiki/images/math/9/2/8/928e3bb757ff68756ec97a0a9d8ad16d.png)
V zadnjem izrazu 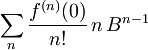 pa prepoznamo ravno odvod
pa prepoznamo ravno odvod 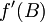 . Rezultat je torej
. Rezultat je torej
![[A,\, f(B)] = f'(B)\,[A,B]](/wiki/images/math/1/1/7/11758588564e29603d3260f5fadff7f5.png)
b) Naša naslednja naloga je bila pokazati, da velja ![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png) , če
, če ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) komutira z operatorjema
komutira z operatorjema 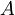 in
in 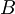 , torej
, torej ![[[A,B],\,A]=0](/wiki/images/math/8/9/9/899c97e1454e46f9bb4f4eb4b422062c.png) in
in ![[[A,B],\,B]=0](/wiki/images/math/7/5/c/75c52f93077726a13d472531934ec151.png) .
.
Naloge se lotimo tako, da vpeljemo funkcijo 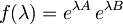 in izračunamo odvod te funkcije:
in izračunamo odvod te funkcije:
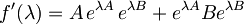
Tu moramo seveda paziti, da operatorja 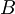 ne nesemo pred eksponent, saj ni nujno, da komutira z
ne nesemo pred eksponent, saj ni nujno, da komutira z 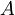 . Zato si pomagamo z enačbo:
. Zato si pomagamo z enačbo:
![[e^{\lambda A}, B] = - [B, e^{\lambda A}] = - \lambda \, e^{\lambda A} [B,A] = \lambda\, e^{\lambda A} [A,B]](/wiki/images/math/b/1/3/b1339f207a8c0a88a1243cb3fcc2ce4e.png)
Tu smo uporabili rezultat iz prejšnjega dela 2. naloge, ![[B,\, f(A)] = f'(A)\,[B,A]](/wiki/images/math/2/1/5/2154e03a9939906e9ed27a0470a8bef5.png) . Seveda pa lahko že prvi komutator zapišemo kot
. Seveda pa lahko že prvi komutator zapišemo kot ![[e^{\lambda A}, B] = e^{\lambda A}\,B - B\,e^{\lambda A}](/wiki/images/math/9/d/4/9d48b982d179ac42b161805b30838629.png) . Če to dvoje potem izenačimo, lahko izrazimo
. Če to dvoje potem izenačimo, lahko izrazimo
![e^{\lambda A}\,B =B\,e^{\lambda A} + \lambda\, e^{\lambda A} [A,B]](/wiki/images/math/a/f/4/af46b492a8dbb06555eeae6e92ad719f.png)
Sedaj se vrnemo nazaj na 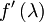 , ki ga lahko z novimi izrazi zapišemo kot
, ki ga lahko z novimi izrazi zapišemo kot
![f'(\lambda ) = A\,e^{\lambda A} \, e^{\lambda B} + (B\, e^{\lambda A} + \lambda e^{\lambda A} [A,B]) e^{\lambda B} = (A + B + \lambda [A,B]) e^{\lambda A} \, e^{\lambda B} = (A + B + \lambda [A,B]) f (\lambda)](/wiki/images/math/3/8/8/388d39934af2225353821dfaa246350c.png)
Tu pa komutator ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) lahko nesem pred eksponent, saj se da eksponent
lahko nesem pred eksponent, saj se da eksponent 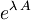 zapisati v Taylorjevo vrsto, v kateri nastopajo potence operatorja
zapisati v Taylorjevo vrsto, v kateri nastopajo potence operatorja 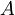 , s katerim po predpostavki komutator
, s katerim po predpostavki komutator ![[A,\,B]](/wiki/images/math/6/b/8/6b8a4f9f3cdf970b697add53a8925762.png) komutira.
komutira.
Dobimo diferencialno enačbo prvega reda, ki ima rešitev
![\ln( f(\lambda)) = (A+B)\lambda + [A,B] \frac{\lambda ^2}{2} + \ln C](/wiki/images/math/2/a/5/2a5d4d86d03832a86af08def80dcfe6c.png)
![f(\lambda) = C e^{(A+B)\lambda + [A,B] \frac{\lambda ^2}{2}}](/wiki/images/math/f/8/6/f86a7ce5322d68b4129cb18bab6896ae.png)
Konstanto C določimo, če postavimo 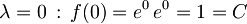
Če postavimo za 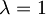 pa dobimo željen rezultat:
pa dobimo željen rezultat:
![f(1) = e^{(A+B)}e^{[A,B] \frac{1}{2}} = e^A\,e^B](/wiki/images/math/6/0/1/6012478b583ed330653aa29060cda282.png)
Tukaj smo zopet uporabili dejstvo, da se da eksponentno funkcijo razviti v Taylorjevo vrsto, kjer se da vsoto po dveh indeksih pretvoriti na produkt dveh vsot. Zato lahko eksponent vsote pišemo kot produkt dveh eksponentov. Zadnjo enačbo se da zapisati tudi kot
![e^{A+B}=e^A e^B e^{-{\frac{1}{2}[A,B]}}](/wiki/images/math/5/0/c/50c6513627928e98e5fbf00bcedcba38.png)
kar smo pravzaprav hoteli pokazati.
c) Zadnja naloga je od nas zahtevala, da dokažemo Baker-Hausdorffovo identiteto: ![e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}](/wiki/images/math/6/9/5/695bedf4d6987cfb532bb2dd921e9629.png) .
.