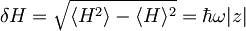Koherentna stanja harmonskega oscilatorja I

Iz Kvantna Mehanika I 2006 - 2007

(Primerjava redakcij)

Trenutna redakcija

Vsebina

1 Naloga
2 Rešitev

[spremeni] Naloga

Za delec v koherentnem stanju 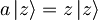$a\left|z\right\rangle=z\left|z\right\rangle$ harmonskega oscilatorja 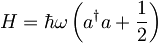$H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right)$ izračunaj nedoločenosti položaja, gibalne količine in energije.

[spremeni] Rešitev

[spremeni] Nedoločenost koordinate

Lego opišemo z

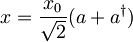$x=\frac{x_{0}}{\sqrt{2}}(a+a^\dagger)$ , kjer je

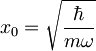$x_{0}=\sqrt{\frac{\hbar}{m\omega}}$ .

Povprečna vrednost lege:

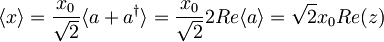$\langle x\rangle=\frac{x_{0}}{\sqrt{2}}\langle a+a^\dagger\rangle=\frac{x_{0}}{\sqrt{2}}2 Re \langle a\rangle=\sqrt{2}x_{0}Re(z)$ ,

zadnji korak pojasni zveza:

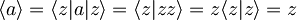$\langle a \rangle= \langle z |a|z\rangle=\langle z|zz \rangle=z\langle z|z \rangle=z$ .

Povprečna vrednost kvadrata lege:

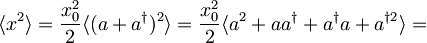
$\langle x^2\rangle = \frac{x_{0}^2}{2}\langle (a+a^\dagger)^2\rangle= \frac{x_{0}^2}{2}\langle a^2+aa^\dagger+a^\dagger a + a^{\dagger 2}\rangle=$

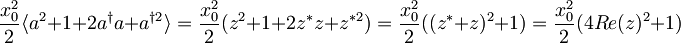
$\frac{x_{0}^{2}}{2}\langle a^2+1+2a^\dagger a+a^{\dagger 2}\rangle= \frac{x_{0}^{2}}{2}(z^2+1+2z^*z+z^{*2})= \frac{x_{0}^{2}}{2}((z^*+z)^2+1)= \frac{x_{0}^{2}}{2}(4Re(z)^2+1)$

Drugi člen izrazimo z zvezo 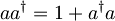$aa^\dagger=1+a^\dagger a$ , tako da je v produktu anihilacijski operator pred kreacijskim.

Ker so koherentna stanja lastna stanja anihilacijskega operatorja jih lahko izrazimo iz anihilacijskega operatorja preko:

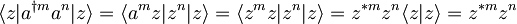
$\langle z|a^{\dagger m}a^{n}|z\rangle = \langle a^m z|z^n|z\rangle = \langle z^m z|z^n|z \rangle =z^{*m}z^n\langle z|z \rangle = z^{*m}z^n$

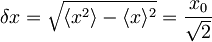
Nedoločenost lege je: $\delta x= \sqrt{\langle x^2\rangle -\langle x\rangle^2}=\frac{x_{0}}{\sqrt{2}}$

[spremeni] Nedoločenost gibalne količine

Na podoben način dobimo nedoločenost gibalne količine.

Operator gibalne količine 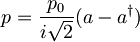$p=\frac{p_{0}}{i \sqrt{2}}(a-a^\dagger)$ , kjer je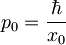 $p_{0}=\frac{\hbar}{x_{0}}$

Povprečna vrednost gibalne količine:

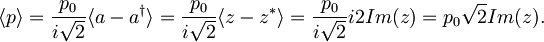
$\langle p\rangle =\frac{p_{0}}{i \sqrt{2}} \langle a-a^\dagger \rangle=\frac{p_{0}}{i \sqrt{2}} \langle z-z^* \rangle= \frac{p_{0}}{i \sqrt{2}}i 2Im(z)=p_{0} \sqrt{2}Im(z).$

Povprečje kvadrata gibalne količine:

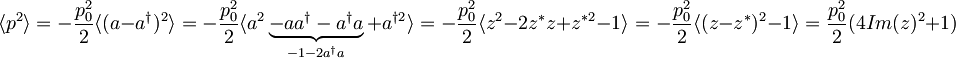
$\langle p^2\rangle =-\frac{p_{0}^{2}}{2} \langle (a-a^\dagger)^2 \rangle= -\frac{p_{0}^{2}}{2}\langle a^2 \underbrace{-aa^\dagger-a^\dagger a}_{-1-2a^\dagger a}+a^{\dagger 2} \rangle= -\frac{p_{0}^{2}}{2}\langle z^2 - 2z^*z+z^{*2}-1 \rangle= -\frac{p_{0}^{2}}{2}\langle (z-z^{*})^2-1\rangle = \frac{p_{0}^{2}}{2}(4Im(z)^2+1)$

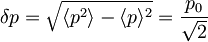
Nedoločenost gibalne količine je: $\delta p= \sqrt{\langle p^2\rangle -\langle p\rangle^2}=\frac{p_{0}}{\sqrt{2}}$

Heisenbergovo načelo nedoločljivosti pokaže, da pri koherentih stanjih velja enakost zveze:

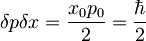
$\delta p\delta x = \frac{x_{0}p_{0}}{2}=\frac{\hbar}{2}$

[spremeni] Nedoločenost energije

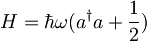
Operator energije $H = \hbar \omega (a^\dagger a + \frac{1}{2})$

Povprečna vrednost energije

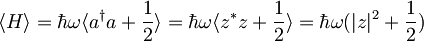
$\langle H\rangle =\hbar \omega \langle a^\dagger a +\frac{1}{2} \rangle= \hbar \omega \langle z^* z +\frac{1}{2} \rangle= \hbar \omega (|z|^2 +\frac{1}{2})$

Povprečna vrednost kvadrata energije:

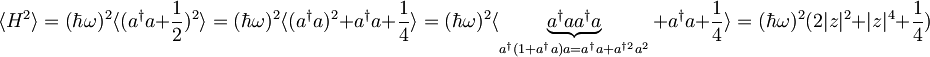
$\langle H^2\rangle = (\hbar \omega)^2 \langle (a^\dagger a +\frac{1}{2})^2 \rangle= (\hbar \omega)^2 \langle (a^\dagger a)^2 + a^\dagger a +\frac{1}{4}\rangle= (\hbar \omega)^2 \langle \underbrace{a^\dagger a a^\dagger a}_{a^\dagger(1+ a^\dagger a )a=a^\dagger a + a^{\dagger 2}a^2}+ a^\dagger a +\frac{1}{4}\rangle= (\hbar \omega)^2 (2|z|^2 + |z|^4 + \frac{1}{4} )$

Nedoločenost energije je:

$\delta H= \sqrt{\langle H^2\rangle -\langle H\rangle^2}=\hbar \omega |z|$

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Koherentna_stanja_harmonskega_oscilatorja_I«

 -\frac{p_{0}^{2}}{2}\langle a^2 \underbrace{-aa^\dagger-a^\dagger a}_{-1-2a^\dagger a}+a^{\dagger 2} \rangle=
 -\frac{p_{0}^{2}}{2}\langle z^2 - 2z^*z+z^{*2}-1 \rangle=
--\frac{p_{0}^{2}}{2}\langle (z-z*)^2-1\rangle =
+-\frac{p_{0}^{2}}{2}\langle (z-z^{*})^2-1\rangle =
 \frac{p_{0}^{2}}{2}(4Im(z)^2+1)</math>
 <math>\langle H^2\rangle = (\hbar \omega)^2 \langle (a^\dagger a +\frac{1}{2})^2 \rangle=
 (\hbar \omega)^2 \langle (a^\dagger a)^2 + a^\dagger a  +\frac{1}{4}\rangle=
-(\hbar \omega)^2 \langle \underbrace{a^\dagger a a^\dagger a}_{a^\dagger(1+ a^\dagger a )a=aa^\dagger + a^{\dagger 2}a^2}+ a^\dagger a  +\frac{1}{4}\rangle=
+(\hbar \omega)^2 \langle \underbrace{a^\dagger a a^\dagger a}_{a^\dagger(1+ a^\dagger a )a=a^\dagger a + a^{\dagger 2}a^2}+ a^\dagger a  +\frac{1}{4}\rangle=
 (\hbar \omega)^2 (2|z|^2 + |z|^4 + \frac{1}{4} ) </math>