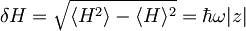Koherentna stanja harmonskega oscilatorja I
Iz Kvantna Mehanika I 2006 - 2007
| Redakcija: 11:18, 26 marec 2007 (spremeni) WikiSysop (Pogovor | prispevki) (New page: == Naloga == == Rešitev ==) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (20:36, 24 maj 2007) (spremeni) (undo) 193.95.248.110 (Pogovor) |
||
| ( not shown.) | |||
| Vrstica 1: | Vrstica 1: | ||
| == Naloga == | == Naloga == | ||
| + | |||
| + | Za delec v koherentnem stanju <math>a\left|z\right\rangle=z\left|z\right\rangle</math> harmonskega oscilatorja <math>H=\hbar\omega\left(a^\dagger a+\frac{1}{2}\right)</math> izračunaj nedoločenosti položaja, gibalne količine in energije. | ||
| == Rešitev == | == Rešitev == | ||
| + | |||
| + | ====Nedoločenost koordinate==== | ||
| + | |||
| + | Lego opišemo z | ||
| + | |||
| + | <math>x=\frac{x_{0}}{\sqrt{2}}(a+a^\dagger)</math>, kjer je | ||
| + | |||
| + | <math>x_{0}=\sqrt{\frac{\hbar}{m\omega}}</math>. | ||
| + | |||
| + | Povprečna vrednost lege: | ||
| + | |||
| + | <math>\langle x\rangle=\frac{x_{0}}{\sqrt{2}}\langle a+a^\dagger\rangle=\frac{x_{0}}{\sqrt{2}}2 Re \langle a\rangle=\sqrt{2}x_{0}Re(z) </math>, | ||
| + | |||
| + | zadnji korak pojasni zveza: | ||
| + | |||
| + | <math> \langle a \rangle= \langle z |a|z\rangle=\langle z|zz \rangle=z\langle z|z \rangle=z</math>. | ||
| + | |||
| + | Povprečna vrednost kvadrata lege: | ||
| + | |||
| + | <math>\langle x^2\rangle = \frac{x_{0}^2}{2}\langle (a+a^\dagger)^2\rangle= | ||
| + | \frac{x_{0}^2}{2}\langle a^2+aa^\dagger+a^\dagger a + a^{\dagger 2}\rangle=</math> | ||
| + | |||
| + | <math>\frac{x_{0}^{2}}{2}\langle a^2+1+2a^\dagger a+a^{\dagger 2}\rangle= | ||
| + | \frac{x_{0}^{2}}{2}(z^2+1+2z^*z+z^{*2})= | ||
| + | \frac{x_{0}^{2}}{2}((z^*+z)^2+1)= | ||
| + | \frac{x_{0}^{2}}{2}(4Re(z)^2+1)</math> | ||
| + | |||
| + | Drugi člen izrazimo z zvezo <math>aa^\dagger=1+a^\dagger a</math>, | ||
| + | tako da je v produktu anihilacijski operator pred kreacijskim. | ||
| + | |||
| + | Ker so koherentna stanja lastna stanja anihilacijskega operatorja jih lahko izrazimo iz | ||
| + | anihilacijskega operatorja preko: | ||
| + | |||
| + | <math>\langle z|a^{\dagger m}a^{n}|z\rangle = \langle a^m z|z^n|z\rangle = | ||
| + | \langle z^m z|z^n|z \rangle =z^{*m}z^n\langle z|z \rangle = z^{*m}z^n</math> | ||
| + | |||
| + | |||
| + | Nedoločenost lege je: | ||
| + | <math>\delta x= \sqrt{\langle x^2\rangle -\langle x\rangle^2}=\frac{x_{0}}{\sqrt{2}}</math> | ||
| + | |||
| + | |||
| + | ====Nedoločenost gibalne količine==== | ||
| + | |||
| + | Na podoben način dobimo nedoločenost gibalne količine. | ||
| + | |||
| + | Operator gibalne količine <math>p=\frac{p_{0}}{i \sqrt{2}}(a-a^\dagger) </math>, kjer je <math> p_{0}=\frac{\hbar}{x_{0}}</math> | ||
| + | |||
| + | Povprečna vrednost gibalne količine: | ||
| + | |||
| + | <math> \langle p\rangle =\frac{p_{0}}{i \sqrt{2}} \langle a-a^\dagger \rangle=\frac{p_{0}}{i \sqrt{2}} \langle z-z^* \rangle= | ||
| + | \frac{p_{0}}{i \sqrt{2}}i 2Im(z)=p_{0} \sqrt{2}Im(z).</math> | ||
| + | |||
| + | Povprečje kvadrata gibalne količine: | ||
| + | |||
| + | <math> \langle p^2\rangle =-\frac{p_{0}^{2}}{2} \langle (a-a^\dagger)^2 \rangle= | ||
| + | -\frac{p_{0}^{2}}{2}\langle a^2 \underbrace{-aa^\dagger-a^\dagger a}_{-1-2a^\dagger a}+a^{\dagger 2} \rangle= | ||
| + | -\frac{p_{0}^{2}}{2}\langle z^2 - 2z^*z+z^{*2}-1 \rangle= | ||
| + | -\frac{p_{0}^{2}}{2}\langle (z-z^{*})^2-1\rangle = | ||
| + | \frac{p_{0}^{2}}{2}(4Im(z)^2+1)</math> | ||
| + | |||
| + | Nedoločenost gibalne količine je: | ||
| + | <math>\delta p= \sqrt{\langle p^2\rangle -\langle p\rangle^2}=\frac{p_{0}}{\sqrt{2}}</math> | ||
| + | |||
| + | Heisenbergovo načelo nedoločljivosti pokaže, da pri koherentih stanjih velja enakost zveze: | ||
| + | |||
| + | <math>\delta p\delta x = \frac{x_{0}p_{0}}{2}=\frac{\hbar}{2}</math> | ||
| + | |||
| + | |||
| + | ====Nedoločenost energije==== | ||
| + | |||
| + | |||
| + | Operator energije | ||
| + | <math> H = \hbar \omega (a^\dagger a + \frac{1}{2})</math> | ||
| + | |||
| + | Povprečna vrednost energije | ||
| + | |||
| + | <math> \langle H\rangle =\hbar \omega \langle a^\dagger a +\frac{1}{2} \rangle= | ||
| + | \hbar \omega \langle z^* z +\frac{1}{2} \rangle= | ||
| + | \hbar \omega (|z|^2 +\frac{1}{2})</math> | ||
| + | |||
| + | Povprečna vrednost kvadrata energije: | ||
| + | |||
| + | <math>\langle H^2\rangle = (\hbar \omega)^2 \langle (a^\dagger a +\frac{1}{2})^2 \rangle= | ||
| + | (\hbar \omega)^2 \langle (a^\dagger a)^2 + a^\dagger a +\frac{1}{4}\rangle= | ||
| + | (\hbar \omega)^2 \langle \underbrace{a^\dagger a a^\dagger a}_{a^\dagger(1+ a^\dagger a )a=a^\dagger a + a^{\dagger 2}a^2}+ a^\dagger a +\frac{1}{4}\rangle= | ||
| + | |||
| + | (\hbar \omega)^2 (2|z|^2 + |z|^4 + \frac{1}{4} ) </math> | ||
| + | |||
| + | Nedoločenost energije je: | ||
| + | |||
| + | <math>\delta H= \sqrt{\langle H^2\rangle -\langle H\rangle^2}=\hbar \omega |z|</math> | ||
Trenutna redakcija
Vsebina |
[spremeni] Naloga
Za delec v koherentnem stanju 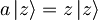 harmonskega oscilatorja
harmonskega oscilatorja 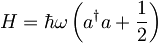 izračunaj nedoločenosti položaja, gibalne količine in energije.
izračunaj nedoločenosti položaja, gibalne količine in energije.
[spremeni] Rešitev
[spremeni] Nedoločenost koordinate
Lego opišemo z
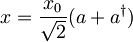 , kjer je
, kjer je
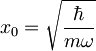 .
.
Povprečna vrednost lege:
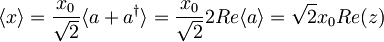 ,
,
zadnji korak pojasni zveza:
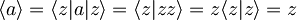 .
.
Povprečna vrednost kvadrata lege:
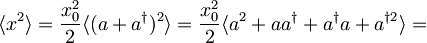
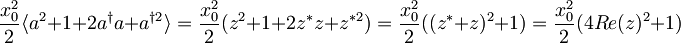
Drugi člen izrazimo z zvezo 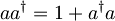 ,
tako da je v produktu anihilacijski operator pred kreacijskim.
,
tako da je v produktu anihilacijski operator pred kreacijskim.
Ker so koherentna stanja lastna stanja anihilacijskega operatorja jih lahko izrazimo iz anihilacijskega operatorja preko:
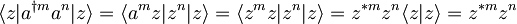
Nedoločenost lege je:
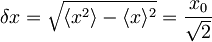
[spremeni] Nedoločenost gibalne količine
Na podoben način dobimo nedoločenost gibalne količine.
Operator gibalne količine 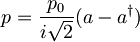 , kjer je
, kjer je 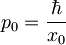
Povprečna vrednost gibalne količine:
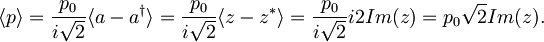
Povprečje kvadrata gibalne količine:
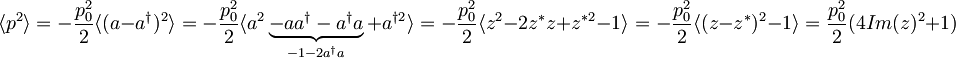
Nedoločenost gibalne količine je:
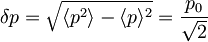
Heisenbergovo načelo nedoločljivosti pokaže, da pri koherentih stanjih velja enakost zveze:
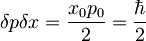
[spremeni] Nedoločenost energije
Operator energije
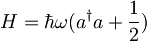
Povprečna vrednost energije
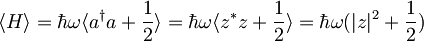
Povprečna vrednost kvadrata energije:
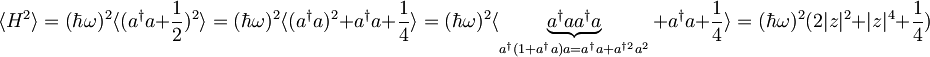
Nedoločenost energije je: