Neskončna potencialna jama

(Primerjava redakcij)

Redakcija: 21:52, 16 februar 2007

Pokaži, da imajo lastne funkcije dobro določeno parnost - so ali sode ali lihe, če je potencial sod 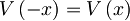$V\left(-x\right)=V\left(x\right)$ in so lastna stanja nedegenerirana.
Poišči lastne energije in lastne funkcije delca v neskončni potencialni jami z dolžino $a$ .
Delec v neskončni potencialni jami z dolžino a ob času t = 0 opišemo z valovno funkcijo
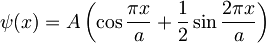$\psi(x)=A\left(\cos\frac{\pi x}{a}+\frac{1}{2}\sin\frac{2\pi x}{a}\right)$ .
- Normaliziraj valovno funkcijo.
- Izračunaj časovni razvoj valovne funkcije.
- Kako se s časom spreminja verjetnost, da se delec nahaja v desni polovici potencialne jame?
- Izračunaj časovno odvisnost pričakovane vrednosti položaja in gibalne količine delca.
- Kako sta ti dve količini povezani?

Redakcija: 21:48, 16 februar 2007 (spremeni) WikiSysop (Pogovor \| prispevki) ← Pojdi na prejšnje urejanje		Redakcija: 21:52, 16 februar 2007 (spremeni) (undo) WikiSysop (Pogovor \| prispevki) Novejše urejanje →
Vrstica 12:		Vrstica 12:

	== Rešitev ==		== Rešitev ==
-
-	test