Neskončna potencialna jama

Iz Kvantna Mehanika I 2006 - 2007

[spremeni] Naloga

Pokaži, da imajo lastne funkcije dobro določeno parnost - so ali sode ali lihe, če je potencial sod 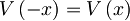$V\left(-x\right)=V\left(x\right)$ in so lastna stanja nedegenerirana.
Poišči lastne energije in lastne funkcije delca v neskončni potencialni jami z dolžino $a$ .
Delec v neskončni potencialni jami z dolžino a ob času t = 0 opišemo z valovno funkcijo
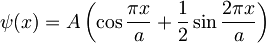$\psi(x)=A\left(\cos\frac{\pi x}{a}+\frac{1}{2}\sin\frac{2\pi x}{a}\right)$ .
- Normaliziraj valovno funkcijo.
- Izračunaj časovni razvoj valovne funkcije.
- Kako se s časom spreminja verjetnost, da se delec nahaja v desni polovici potencialne jame?
- Izračunaj časovno odvisnost pričakovane vrednosti položaja in gibalne količine delca.
- Kako sta ti dve količini povezani?

[spremeni] Rešitev

Če je potencial sod, potem je soda tudi Hamiltonova funkcija:

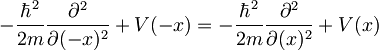
$-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial(-x)^2} + V(-x) = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial(x)^2} + V(x)$

Če imamo lastno funkcijo Hamiltonovega operatorja z neko energijo E (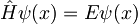 $\hat{H} \psi(x) = E \psi(x)$ ), potem ima 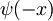$\psi(-x)\,\!$ isto energijo: 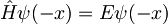$\hat{H} \psi(-x) = E \psi(-x)$ . Ker smo predpostavili, da stanja niso degenerirana, sta funkciji sorazmerni s kompleksno konstanto $c\,\!$ :

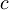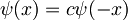
$\psi(x) = c \psi(-x)\,\!$

Zamenjajmo 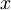$x\,\!$ z $-x\,\!$ :

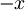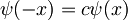
$\psi(-x) = c \psi(x)\,\!$

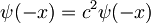
in to vstavimo v prejšnjo enačbo da dobimo $\psi(-x) = c^2 \psi(-x)\,\!$

Očitno mora biti kvadrat kompleksnega števila 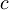$c\,\!$ enak ena, kar pomeni 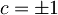$c = \pm 1\,\!$ . Torej morajo biti lastne funkcije v takem potencialu nujno sode ali lihe.

V neskončni potencialni jami je potencial oblike

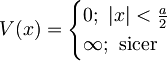
$V(x) = \begin{cases} 0;\ |x|<\frac{a}{2} \\ \infty;\ \mathrm{sicer} \end{cases}$

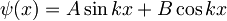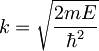Tedaj je splošna rešitev stacionarne Schrödingerjeve enačbe oblike $\psi(x) = A\sin kx + B\cos kx\,\!$ , kjer je $k = \sqrt{\frac{2mE}{\hbar^2}}$ , m je masa delca, E pa njegova energija.

Zunaj jame se delec ne more nahajati, saj bi moral imeti neskončno energijo, torej je tam vrednost valovne funkcije enaka 0. To pomeni, da mora biti zaradi zveznosti tudi na robovih jame 0, kar nam da robna pogoja, iz katerih lahko določimo manjkajoče konstante.

Najprej si izberimo B=0.

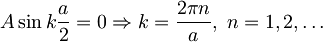
$A \sin k\frac{a}{2} = 0 \Rightarrow k = \frac{2\pi n}{a},\ n=1,2,\dots$

Konstanto A dobimo iz normalizacije te funkcije:

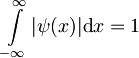
$\int\limits_{-\infty}^{\infty} |\psi(x)| \mbox{d}x = 1$

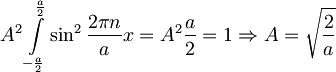
$A^2 \int\limits_{-\frac{a}{2}}^{\frac{a}{2}} \sin^2 \frac{2\pi n}{a}x = A^2\frac{a}{2} = 1 \Rightarrow A=\sqrt{\frac{2}{a}}$

Zdaj postavimo A=0.

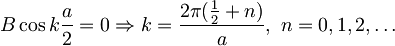
$B \cos k\frac{a}{2} = 0 \Rightarrow k = \frac{2\pi (\frac{1}{2}+n)}{a},\ n=0,1,2,\dots$

Normalizacija te funkcije nam da B=A.

Tako imamo dva nabora lastnih funkcij, katerih zapis lahko poenotimo kot

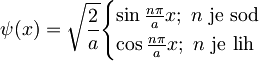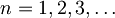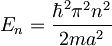$\psi(x) = \sqrt{\frac{2}{a}}\begin{cases} \sin \frac{n\pi}{a}x;\ n\text{ je sod}\\ \cos \frac{n\pi}{a}x;\ n\text{ je lih} \end{cases}$ , kjer je $n=1,2,3,\dots$ Ta stanja imajo energijo $E_n=\frac{\hbar^2\pi^2n^2}{2ma^2}$ .

Poglejmo si funkcijo 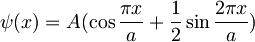$\psi(x) = A(\cos\frac{\pi x}{a} + \frac{1}{2}\sin\frac{2\pi x}{a})$

Vsako valovno funkcijo lahko razvijemo po lastnih funkcijah sistema. Tukaj hitro vidimo, da gre za prvi dve lastni funkciji. V prej definiranem zapisu lahko torej zapišemo

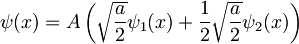
$\psi(x) = A\left(\sqrt{\frac{a}{2}}\psi_1(x)+\frac{1}{2}\sqrt{\frac{a}{2}}\psi_2(x)\right)$

Določimo normalizacijsko konstanto:

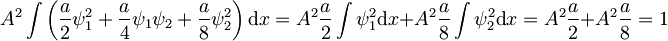
$A^2\int\left(\frac{a}{2}\psi_1^2 + \frac{a}{4}\psi_1\psi_2 + \frac{a}{8}\psi_2^2\right)\mbox{d}x = A^2\frac{a}{2}\int \psi_1^2\mbox{d}x + A^2\frac{a}{8}\int\psi_2^2\mbox{d}x = A^2\frac{a}{2} + A^2\frac{a}{8} = 1$

Tu smo upoštevali ortonormiranost lastnih funkcij: integral mešanega člena je nič, integral kvadratov pa ena.

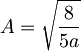
$A=\sqrt{\frac{8}{5a}}$

Verjetnost, da se delec nahaja na nekem intervalu, dobimo z integracijo gostote verjetnosti po tem intervalu. Ta verjetnost je seveda odvisna od časa, zato bomo uporabili od časa odvisno valovno funkcijo.

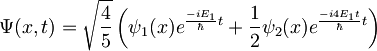$\Psi(x,t) = \sqrt{\frac{4}{5}} \left(\psi_1(x) e^{\frac{-iE_1}{\hbar}t} + \frac{1}{2}\psi_2(x) e^{\frac{-i4E_1t}{\hbar}t}\right)$ , kjer smo že upoštevali $E 2 = 4 E 1$

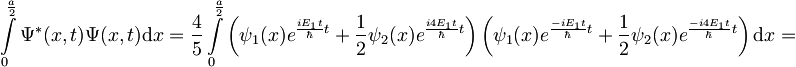
$\int\limits_0^{\frac{a}{2}}\Psi^*(x,t)\Psi(x,t)\mbox{d}x = \frac{4}{5} \int\limits_0^{\frac{a}{2}} \left(\psi_1(x)e^{\frac{iE_1t}{\hbar}t} + \frac{1}{2} \psi_2(x)e^{\frac{i4E_1t}{\hbar}t}\right) \left(\psi_1(x)e^{\frac{-iE_1t}{\hbar}t} + \frac{1}{2} \psi_2(x)e^{\frac{-i4E_1t}{\hbar}t}\right)\mbox{d}x=$

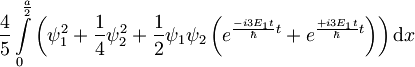
$\frac{4}{5}\int\limits_0^{\frac{a}{2}}\left(\psi_1^2+\frac{1}{4}\psi_2^2+\frac{1}{2}\psi_1\psi_2\left( e^{\frac{-i3E_1t}{\hbar}t} + e^{\frac{+i3E_1t}{\hbar}t}\right)\right)\mbox{d}x$

Eksponenta lahko pretvorimo v kosinus:

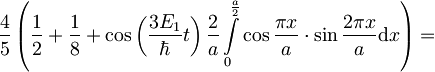
$\frac{4}{5}\left(\frac{1}{2}+\frac{1}{8}+ \cos\left(\frac{3E_1}{\hbar}t\right)\frac{2}{a} \int\limits_0^{\frac{a}{2}}\cos\frac{\pi x}{a} \cdot \sin\frac{2\pi x}{a}\mbox{d}x \right)=$

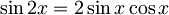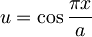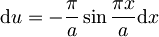Uporabimo pravilo $\sin 2x=2\sin x\cos x\,\!$ in uvedemo substitucijo $u=\cos\frac{\pi x}{a}$ , $\mbox{d}u=-\frac{\pi}{a}\sin\frac{\pi x}{a}\mbox{d}x$ .

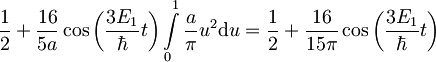
$\frac{1}{2} + \frac{16}{5a}\cos\left(\frac{3E_1}{\hbar}t\right)\int\limits_0^1\frac{a}{\pi}u^2\mbox{d}u= \frac{1}{2}+\frac{16}{15\pi}\cos\left(\frac{3E_1}{\hbar}t\right)$

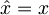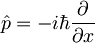Pričakovano vrednost položaja in gibalne količine izračunamo s pomočjo operatorjev $\hat{x}=x\,\!$ in $\hat{p}=-i\hbar\frac{\partial}{\partial x}\,\!$ . Račun je nekoliko daljši in nezanimiv, zato ga tu ne bomo delali. Rezultat je

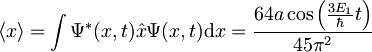
$\langle x\rangle = \int\Psi^*(x,t)\hat{x}\Psi(x,t)\mbox{d}x = \frac{64a\cos\left(\frac{3E_1}{\hbar}t\right)}{45\pi^2}$

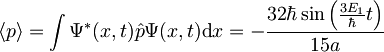
$\langle p\rangle = \int\Psi^*(x,t)\hat{p}\Psi(x,t)\mbox{d}x = -\frac{32\hbar\sin\left(\frac{3E_1}{\hbar}t\right)}{15a}$

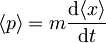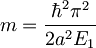Vidimo, da velja $\langle p\rangle = m\frac{\mbox{d}\langle x\rangle}{\mbox{d}t}$ za $m=\frac{\hbar^2\pi^2}{2a^2E_1}$ . Za pričakovano vrednost gibalne količine velja torej klasična zveza.

Vzpostavljeno iz »http://burana.ijs.si/wiki/index.php/Neskon%C4%8Dna_potencialna_jama«