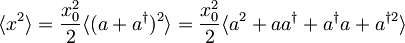Koherentna stanja harmonskega oscilatorja I
Iz Kvantna Mehanika I 2006 - 2007
(Primerjava redakcij)
| Redakcija: 17:59, 29 marec 2007 (spremeni) 193.95.248.110 (Pogovor) ← Pojdi na prejšnje urejanje |
Redakcija: 18:50, 29 marec 2007 (spremeni) (undo) 193.95.248.110 (Pogovor) Novejše urejanje → |
||
| Vrstica 15: | Vrstica 15: | ||
| Povprečna vrednost lege: | Povprečna vrednost lege: | ||
| - | <math>\langle x\rangle=</math> | + | <math>\langle x\rangle=\frac{x_{0}}{\sqrt{2}}\langle a+a^\dagger\rangle=\frac{x_{0}}{\sqrt{2}}2 Re \langle a\rangle=\sqrt{2}x_{0}Re(z) </math>, |
| + | |||
| + | zadnji korak pojasni zveza: | ||
| + | |||
| + | <math> \langle a \rangle= \langle z |a|z\rangle=\langle z|zz \rangle=z\langle z|z \rangle=z</math>. | ||
| + | |||
| + | Povprečna vrednost kvadrata lege: | ||
| + | |||
| + | <math>\langle x^2\rangle = \frac{x_{0}^2}{2}\langle (a+a^\dagger)^2\rangle= | ||
| + | \frac{x_{0}^2}{2}\langle a^2+aa^\dagger+a^\dagger a + a^{\dagger 2}\rangle</math> | ||
Redakcija: 18:50, 29 marec 2007
Naloga
Za delec v koherentnem stanju 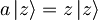 harmonskega oscilatorja
harmonskega oscilatorja 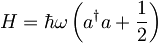 izračunaj nedoločenosti položaja, gibalne količine in energije.
izračunaj nedoločenosti položaja, gibalne količine in energije.
Rešitev
Nedoločenost koordinate
Lego opišemo z
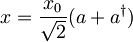 , kjer je
, kjer je
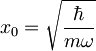 .
.
Povprečna vrednost lege:
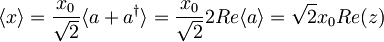 ,
,
zadnji korak pojasni zveza:
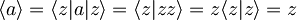 .
.
Povprečna vrednost kvadrata lege: