7. Linearna regresija

Iz Računalniška orodja v fiziki 2008 - 2009

Redakcija iz 18:13, 20. april 2009 od Asistent (Pogovor | prispevki)

(prim) ← Starejša redakcija | poglejte trenutno redakcijo (prim) | Novejša redakcija → (prim)

Linearna zveza $y = k x$ je najpreprostejša in najpogostejša zveza med dvema fizikalnima količinama, zlasti še, ker lahko tudi druge funkcijske odvisnosti v ozkem intervalu aproksimiramo z linearno zvezo: $Δ y = k Δ x$ . Vemo, da sorazmernostni koeficient $k$ za majhne $Δ x$ limitira k odvodu $d y / d x$ .

Kadar moramo določiti koeficient v linearni zvezi dveh količin $x$ in $y$ , je s stališča merske tehnike koristno izmeriti več kot en par $(x, y)$ . Če določimo vrednosti $y i$ , ki ustrezajo celi vrsti izbranih $x i$ , $i$ = 1, 2, ..., $m$ , lahko z njimi določimo $k$ z večjo natančnostjo. Obenem preverimo, ali linearna zveza zares velja, pa tudi, ali naša merska naprava dobro deluje v širšem intervalu spremenljivk. Zlasti se lahko zgodi, da ima merilec te ali druge količine premaknjeno ničlo. Tedaj se naša linearna zveza ne pokaže kot premica skozi izhodišče koordinatnega sistema, pač pa je nekoliko premaknjena. Zato velja, da iz vrste meritev $x i$ , $y i$ nikoli ne računamo koeficienta kot povprečje kvocientov $y i / x i$ , pač pa vedno kot naklon premice, ki jo potegnemo skozi izmerjene točke.

Problem najboljše premice skozi dane merske točke je mogoče definirati na mnogo načinov, ki pa se vsi prevedejo na eno od dveh matematičnih oblik. Če smo za meritve že določili korelacijski koeficient (prim. 6.1-2), zadošča vedeti, da gre najboljša premica vedno skozi težišče oblaka točk $(x pov, y pov)$ in da ima naklon $R σ y / σ x$ .

Sicer pa lahko koeficienta $k$ in $n$ najboljše premice $y = k x + n$ določimo tudi z elementarnim računom. Zahtevamo, naj bo vsota kvadratov razdalj točk od premice najmanjša (načelo najmanjših kvadratov – least squares principle):

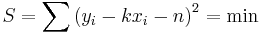$S=\sum\left(y_i-kx_i-n\right)^2=\mathrm{min}$ .

Sistem dveh enačb za $k$ in $n$ rešimo z naslednjim programom:

sum1 := 0; sumx := 0; sumy := 0; sumx2 := 0; sumxy := 0; for i:=1 to m do begin add(sum1, 1); add(sumx, x[i]); add(sumy, y[i]); add(sumx2, x[i]*x[i]); add(sumxy, x[i]*y[i]) end; k := (sum1*sumxy – sumx*sumy)/(sum1*sumx2 – sumx*sumx); n := (sumx2*sumy – sumx*sumxy)/(sum1*sumx2 – sumx*sumx)

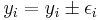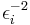V zaresni merilni tehniki se spodobi, da so meritve opremljene s statistično napako, torej $y_i= y_i\pm\epsilon_i$ . Kadar se $ε i$ od izmerka do izmerka znatno spreminja, je teža posameznih točk različna. Statistično neoporečen rezultat dobimo, če v gornjem programu vse sumande utežimo z $\epsilon_i^{-2}$ :

add(sumz, z[i]/sqr(ε[i]));

kjer je z[i] po vrsti 1, x[i], y[i], x[i]*x[i] in x[i]*y[i]. To je druga, popolnejša oblika za najboljšo premico. V njej vsoto $S$ , ki smo jo minimizirali, običajno označimo s $χ 2$ in jo lahko uporabljamo tudi za diagnozo kvalitete ujemanja. Za dobro ujemanje je njena pričakovana vrednost 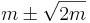$m\pm\sqrt{2m}$ . Govorimo o testu hi-kvadrat.

Mnoga računska orodja imajo že vgrajene ukaze za najboljše premice. Velja preveriti, katero od obeh oblik uporabljajo.

Naloge

Za meritve^[1] v datoteki "HitrostTokaOdFrekvence.txt" (naloga 6.1) določi parametra najboljše premice. Ker so podane napake hitrosti, lahko določiš tudi $χ 2$ .
Skozi oblak podatkov "Tintin.dat" potegni najboljšo premico. Uporabiš lahko kar korelacijske rezultate iz naloge 6.2.
Skozi točke v histogramu podatkov "Interval.dat" poskusi potegniti najboljšo eksponentno funkcijo $w = A e - λ x$ , ki jo moramo najprej predelati v linearno zvezo. Z logaritmiranjem dobimo $ln(w) = ln(A) - λ x$ . V grafu $y = ln(w)$ od $x$ sta koeficienta premice $k = - λ$ in $n = ln(A)$ . Po teoriji verjetnosti mora biti koeficient $λ$ enak recipročni povprečni vrednosti histograma.
Teorija kemijske kinetike napove za sigmoidno krivuljo iz podatkov "Adrenalin.dat" (naloga 1.1) naslednjo odvisnost $F / F max = c / (a + c)$ , kjer pomeni $a$ koncentracijo s polovičnim maksimalnim učinkom. Določi koeficienta $F max$ in $a$ . Pretvori v linearno zvezo – ena pot je uvedba recipročnih spremenljivk $1 / F$ in $1 / c$ , druga pa je uvedba spremenljivke $c / F$ .

Literatura

↑ Blaž Kavčič, Dušan Babič in Igor Poberaj, Mikrofluidično vezje z mikročrpalko, OMF 56 (2009) 1.

[0] Blaž Kavčič, Dušan Babič in Igor Poberaj, Mikrofluidično vezje z mikročrpalko, OMF 56 (2009) 1.

[1]