Heisenbergovo načelo nedoločenosti II
Iz Kvantna mehanika I 2008 - 2009
(Primerjava redakcij)
| Redakcija: 20:43, 19 marec 2009 (spremeni) Asistent (Pogovor | prispevki) (New page: # S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (<math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>).ira z operatorjema ...) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (20:44, 19 marec 2009) (spremeni) (undo) Asistent (Pogovor | prispevki) |
||
| Vrstica 1: | Vrstica 1: | ||
| - | # S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (<math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>).ira z operatorjema <math>A</math> in <math>B</math>. | + | # S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (<math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>). |
| # Dokaži Baker-Hausdorffovo identiteto: <math>e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}</math>. | # Dokaži Baker-Hausdorffovo identiteto: <math>e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}</math>. | ||
Trenutna redakcija
- S pomočjo principa nedoločenosti za lego in gibalno količino oceni energijo osnovnega stanja harmonskega oscilatorja (
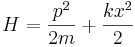 ).
).
- Dokaži Baker-Hausdorffovo identiteto:
![e^A B e^{-A}=B+[A,B]+\frac{1}{2!}[A,[A,B]]+{\ldots}](/wiki7/images/math/6/9/5/695bedf4d6987cfb532bb2dd921e9629.png) .
.