Časovno odvisna perturbacija III
Iz Kvantna mehanika I 2007 - 2008
(Primerjava redakcij)
| Redakcija: 13:36, 8 maj 2008 (spremeni) Asistent (Pogovor | prispevki) m (- prestavitev Spin VII na Časovno odvisna perturbacija III) ← Pojdi na prejšnje urejanje |
Redakcija: 16:38, 11 junij 2008 (spremeni) (undo) Asistent (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 1: | Vrstica 1: | ||
| == Naloga == | == Naloga == | ||
| - | Elektron v homogenem magnetnem polju <math>{\mathbf B_0}=(0,0,B_0)</math> je v osnovnem stanju (zanimamo se samo za spinski del valovne funkcije). Ob času t = 0 na elektron delujemo s sunkom magnetnega polja <math>{\mathbf B}(t)=(B\delta(t), 0,0)</math>. Kolikšna je verjetnost, da je ob času t elektron v vzbujenem stanju? Primerjaj točno rešitev in rezultate perturbacijske teorije. Glej Schwabl, naloga 16.4. | + | Delca s spinoma <math>S_{1}=1</math> in <math>S_{2}=1</math> sta sklopljena s Heisenbergovo interakcijo <math>H=-J\mathbf{S}_{1}\cdot\mathbf{S_{2}}</math>. Z meritvijo, ki jo opravimo ob <math>t=0</math>, ugotovimo, da za valovno funkcijo <math>\left|\psi,0\right\rangle </math> velja <math>S_{1z}\left|\psi,0\right\rangle =\hbar\left|\psi,0\right\rangle </math> in <math>S_{2y}\left|\psi,0\right\rangle =\hbar\left|\psi,0\right\rangle </math>. |
| + | #Zapiši valovno funkcijo ob <math>t=0</math> v produktni bazi. | ||
| + | #Razvij valovno funkcijo po bazi z dobro velikostjo celotnega spina in njegovo projekcijo na os <math>z</math>. | ||
| + | #Zapiši časovni razvoj valovne funkcije. | ||
| + | #Kolikšna je verjetnost, da ob meritvi <math>S_{1z}</math> ob času <math>t>0</math> še vedno dobimo rezultat <math>\hbar</math>? | ||
| == Rešitev == | == Rešitev == | ||
Redakcija: 16:38, 11 junij 2008
Naloga
Delca s spinoma S1 = 1 in S2 = 1 sta sklopljena s Heisenbergovo interakcijo 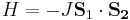 . Z meritvijo, ki jo opravimo ob t = 0, ugotovimo, da za valovno funkcijo
. Z meritvijo, ki jo opravimo ob t = 0, ugotovimo, da za valovno funkcijo 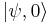 velja
velja 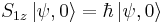 in
in 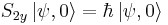 .
.
- Zapiši valovno funkcijo ob t = 0 v produktni bazi.
- Razvij valovno funkcijo po bazi z dobro velikostjo celotnega spina in njegovo projekcijo na os z.
- Zapiši časovni razvoj valovne funkcije.
- Kolikšna je verjetnost, da ob meritvi S1z ob času t > 0 še vedno dobimo rezultat
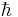 ?
?