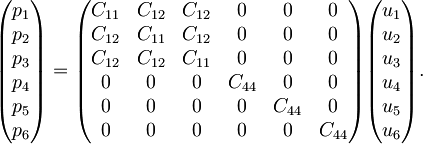Tenzor elastičnosti

Iz Fizika trdne snovi 2007 - 2008

Vsebina

1 Naloga
2 Rešitev

[spremeni] Naloga

Pokaži, da je v splošnem primeru neodvisnih le 21 od 81 elastičnih konstant, ki povezujejo napetost in deformacijo kristala, ter da so v primeru snovi s kubično simetrijo neodvisne le še 3.

[spremeni] Rešitev

[spremeni] Deformacija

Deformacijo zveznega telesa v vsaki točki r opišemo z odmikom od prvotne lege u(r):

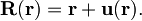
$\mathbf{R}(\mathbf{r})=\mathbf{r}+\mathbf{u}(\mathbf{r}) .$

Ker lahko tako opisani odmiki vključujejo tudi togi premik celotnega telesa, ki nas ne zanima, je v primeru majhnih deformacij smiselno definirati tenzor, ki opisuje spreminjanje komponent deformacije v vsaki kartezični smeri x, y in z kot

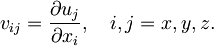
$v_{ij}=\frac{\partial u_j}{\partial x_i} , \quad i, j = x, y, z .$

[spremeni] Napetostni tenzor

Slika 2: Ponazoritev napetosti v telesu.

Pri deformaciji pride v snovi do notranjih napetosti, ki jih opisuje napetostni tenzor p_ij:

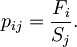
$p_{ij}=\frac{F_i}{S_j}.$

Pove torej, kolikšna sila F v smeri i deluje na namišljeno notranjo ploskev S z normalo v smeri j. V primeru majhnih obremenitev so napetosti v snovi linearno sorazmerne z deformacijo (posplošeni Hookov zakon), le da sorazmernostne elastične konstante, ki povezujejo dva tenzorja drugega reda, sestavljajo tenzor četrtega reda C_ijkl:

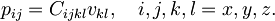
$p_{ij}=C_{ijkl}v_{kl}, \quad i, j, k, l = x, y, z.$

(V zgornji enačbi in v nadaljevanju zaradi lažjega in preglednejšega pisanja upoštevamo sumacijski dogovor o seštevanju po ponovljenih indeksih.) Tenzor C _ijkl ima načeloma 3⁴ = 81 elementov, a bomo v nadaljevanju pokazali, da je v najsplošnejšem primeru neodvisnih le 21 komponent.

Predstavljajmo si majhno kockico v notranjosti deformiranega telesa in poglejmo, kakšne sile delujejo na njene mejne ploskve. Očitno je, da sta nasprotni ploskvi obremenjeni z nasprotnima silama: s kakršno silo deluje okolica na zgornjo ploskvico, s tolikšno deluje tudi spodnja na snov pod njo, slednja pa z nasprotno enako silo nazaj na vmesno – taki pari sil se torej uravnovesijo. Podobno mora veljati za navore, da se košček ne začne vrteti sam od sebe, kar dosežemo z zahtevo o simetričnosti napetostnega tenzorja

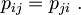
$p_{ij}= p_{ji}\ .$

Od prvotnih 9 komponent je tako neodvisnih le še 6.

[spremeni] Deformacijski tenzor

Zgoraj definirani tenzor v_ij lahko razstavimo na simetrični in antisimetrični del:

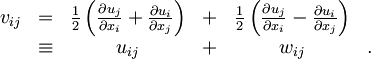
$\begin{matrix} v_{ij} & = & \frac{1}{2} \left( \frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j} \right ) & + & \frac{1}{2} \left( \frac{\partial u_j}{\partial x_i}-\frac{\partial u_i}{\partial x_j} \right ) & \ \\ \ & \equiv & u_{ij} & + & w_{ij} & . \end{matrix}$

Iz elastomehanike se spomnimo, da drugi člen w_ij predstavlja togo rotacijo, tako da splošno deformacijo povsem popiše simetrični deformacijski tenzor u_ij. Tako kot napetostni tenzor p_ij ima tudi deformacijski tenzor u_ij le 6 prostih elementov. Zvezo med tenzorjema lahko z nekoliko spremenjenimi oznakami

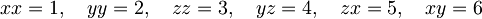
$xx=1, \quad yy=2, \quad zz=3, \quad yz=4, \quad zx=5, \quad xy=6$

lahko prepišemo v bolj pregledno obliko:

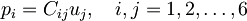
$p_i = C_{ij} u_j , \quad i, j = 1, 2, \dots , 6$

oz. eksplicitno razpisano

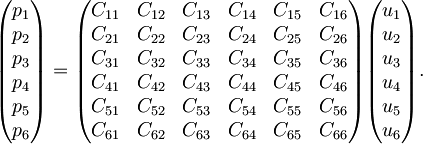
$\begin{pmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \\ p_6 \end{pmatrix} = \begin{pmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ C_{21} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ C_{31} & C_{32} & C_{33} & C_{34} & C_{35} & C_{36} \\ C_{41} & C_{42} & C_{43} & C_{44} & C_{45} & C_{46} \\ C_{51} & C_{52} & C_{53} & C_{54} & C_{55} & C_{56} \\ C_{61} & C_{62} & C_{63} & C_{64} & C_{65} & C_{66} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_5 \\ u_6 \end{pmatrix}.$

Preostalo nam je 36 elastičnih konstant C_ij, ki pa tudi niso vse neodvisne.

[spremeni] Energija deformacije

Elastična energija deformacije vzmeti je v eni dimenziji odvisna od kvadrata raztezka. Tudi za trorazsežno telo je gostota proste energije f kvadratna funkcija deformacij, le da lahko v splošnem nastopajo tudi mešani členi:

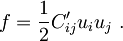
$f = \frac{1}{2}C'_{ij} u_i u_j \ .$

Koeficienti C'_ij so povezani z zgornjimi C_ij, kar bomo videli čez nekaj trenutkov.

Komponente deformacijskega tenzorja lahko enakovredno definiramo tudi kot odvode proste energije po ustreznem elementu deformacijskega tenzorja

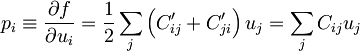
$p_{i} \equiv \frac{\partial f}{\partial u_i} = \frac{1}{2} \sum_{j} \left(C'_{ij}+C'_{ji}\right) u_j = \sum_{j}C_{ij}u_j$

(v tem primeru sumacijski dogovor ne velja, vsota je izpisana eksplicitno). Če rezultat primerjamo s prejšnjo definicijo (zadnji korak zgornje formule), dobimo povezavo med koeficienti C_ij in C'_ij

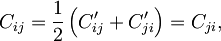
$C_{ij}=\frac{1}{2}\left(C'_{ij}+C'_{ji}\right)=C_{ji},$

od koder sledi, da ima simetričen tenzor C_ij le 21 neodvisnih elementov (6 na diagonali in 15 nad njo), ki predstavljajo 21 elastičnih konstant triklinskih kristalov z najnižjo stopnjo simetrije. Vse dodatne simetrijske zahteve njihovo število še nadalje skrčijo; kot bomo videli v nadaljevanju, ostanejo kristalom s simetrijo kocke le še 3 proste elastične konstante.

[spremeni] Kubična simetrija

Slika 3: Primer rotacije kristala okoli simetrijske osi (111).

Pri nadaljnji redukciji števila konstant bomo uporabili simetrije tro- in štirištevnih osi, ki potekajo po telesnih diagonalah oz. vzdolž stranic kocke. Če zavrtimo smer deformacije za 90° oz. 120° okoli ustrezne simetrijske osi, kristal ne čuti razlike, transformirajo se le koordinate deformacije. V primeru troštevnih osi se to zgodi po sledečih shemah:

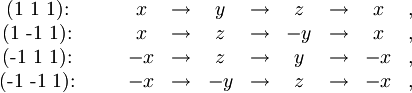
$\begin{matrix} \mbox{(1 1 1):} & \quad & x & \rightarrow & y & \rightarrow & z & \rightarrow & x &,\\ \mbox{(1 -1 1):} &\quad & x & \rightarrow & z & \rightarrow & -y & \rightarrow & x &, \\ \mbox{(-1 1 1):} & \quad & -x & \rightarrow & z & \rightarrow & y & \rightarrow & -x &,\\ \mbox{(-1 -1 1):} & \quad & -x & \rightarrow & -y & \rightarrow & z & \rightarrow & -x &, \end{matrix}$

Zgled: pri drugi rotaciji se komponente deformacijskega tenzorja u_ij transformirajo v u_i'j' kot

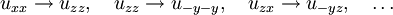
$u_{xx}\rightarrow u_{zz}, \quad u_{zz}\rightarrow u_{-y-y}, \quad u_{zx}\rightarrow u_{-yz}, \quad \dots$

Iz definicije u_ij vidimo, da velja

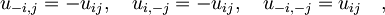
$u_{-i,j}=-u_{ij}, \quad u_{i,-j}=-u_{ij}, \quad u_{-i,-j}=u_{ij} \quad,$

saj deformacija ali odvod v nasprotni smeri oba spremenita predznak elementa. Ker pa se pri takih rotacijah deformacije gostota energije f ne sme spremeniti, smejo v izrazu

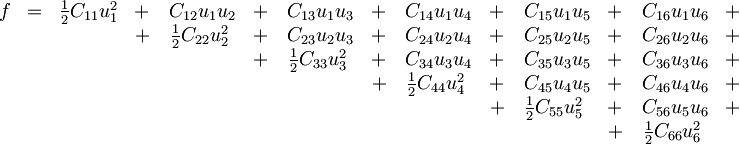
$\begin{matrix} f & = & \frac{1}{2}C_{11} u_1^2 & +\quad C_{12} u_1 u_2 & +\quad C_{13} u_1 u_3 & +\quad C_{14} u_1 u_4 & +\quad C_{15} u_1 u_5 & +\quad C_{16} u_1 u_6 & + \\ \ & \ & \ & +\quad \frac{1}{2}C_{22} u_2^2 \ & +\quad C_{23} u_2 u_3 & +\quad C_{24} u_2 u_4 & +\quad C_{25} u_2 u_5 & +\quad C_{26} u_2 u_6 & + \\ \ & \ & \ & \ & +\quad \frac{1}{2}C_{33} u_3^2 \ & +\quad C_{34} u_3 u_4 & +\quad C_{35} u_3 u_5 & +\quad C_{36} u_3 u_6 & + \\ \ & \ & \ & \ & \ & +\quad \frac{1}{2}C_{44} u_4^2 \ & +\quad C_{45} u_4 u_5 & +\quad C_{46} u_4 u_6 & + \\ \ & \ & \ & \ & \ & \ & +\quad \frac{1}{2}C_{55} u_5^2 \ & +\quad C_{56} u_5 u_6 & + \\ \ & \ & \ & \ & \ & \ & \ & +\quad \frac{1}{2}C_{66} u_6^2 \ \end{matrix}$

nastopati le členi, ki pri nobeni od zgornjih rotacij ne spremenijo predznaka. To lastnost imajo vsi kvadrati elementov u_i² ter produkti med dvema od prvih treh komponent u_iu_j (za i, j = 1, 2, 3, npr. u₁u₂ = u_xxu_yy). Za vse ostale člene lahko najdemo tako rotacijo, ki bo spremenila njihov predznak, zato fizikalno niso sprejemljivi in jim pripišemo koeficiente C_ij = 0:

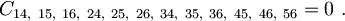
$C_{14,\ 15,\ 16,\ 24,\ 25,\ 26,\ 34,\ 35,\ 36,\ 45,\ 46,\ 56}= 0 \ .$

Tudi v primeru rotacije deformacije okoli štirištevnih osi za $π / 2$ morajo napetosti ostati enake. V primeru rotacije okoli osi x

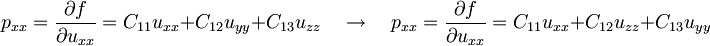
$p_{xx}=\frac{\partial f}{\partial u_{xx}}=C_{11}u_{xx}+C_{12}u_{yy}+C_{13}u_{zz} \quad \rightarrow \quad p_{xx}=\frac{\partial f}{\partial u_{xx}}=C_{11}u_{xx}+C_{12}u_{zz}+C_{13}u_{yy}$

morata biti zadnja dva prispevka prečnih deformacij enakovredna. Z rotacijami okoli ostalih osi ugotovimo, da morajo biti enaki tudi diagonalni prispevki, torej se konstante poenostavijo

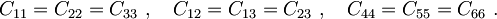
$C_{11}=C_{22}=C_{33}\ , \quad C_{12}=C_{13}=C_{23}\ , \quad C_{44}=C_{55}=C_{66}\ .$

Ostale so nam torej res le 3 neodvisne elastične konstante C₁₁, C₁₂ in C₄₄:

$\begin{pmatrix} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \\ p_6 \end{pmatrix} = \begin{pmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{11} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{12} & C_{11} & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & C_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{44} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \\ u_5 \\ u_6 \end{pmatrix}.$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Tenzor_elasti%C4%8Dnosti«