Bravaisove mreže
Iz Fizika trdne snovi 2007 - 2008
| Redakcija: 17:43, 23 november 2007 (spremeni) Bmikuz (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Redakcija: 19:22, 23 november 2007 (spremeni) (undo) Bmikuz (Pogovor | prispevki) Novejše urejanje → |
||
| Vrstica 1: | Vrstica 1: | ||
| Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje [[Media:14BrM.jpg]] in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže. | Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje [[Media:14BrM.jpg]] in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže. | ||
| + | |||
| + | ==Naloga== | ||
| Mi bi radi na nekaj primerih pokazali, da z dodajanjem novih točk tem Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež. | Mi bi radi na nekaj primerih pokazali, da z dodajanjem novih točk tem Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež. | ||
| - | Vzamemo torej eno od 14 Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo: | + | Vzamemo torej eno od štirinajstih Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo: |
| + | |||
| + | 1.) Ali je še Bravaisova mreža? | ||
| + | |||
| + | 2.) Ali je nova Bravaisova mreža? | ||
| + | |||
| + | =1. Primer:= | ||
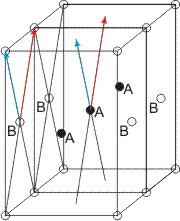
| - | 1. Ali je še Bravaisova mreža? | + | Ortorombske Bravaisove mreže so štiri: simple, base-centered, body-centered in face centered. Zanima nas, če bi dobili novo Bravaisovo mrežo, če bi base-centered mreži dodali še dve točki tako, da bi bile štiri nasprotne ploskve ploskovno centrirane? |
| - | 2.Ali je nova Bravaisova mreža? | + | [[Slika:SLIKA1.jpg]] |
Redakcija: 19:22, 23 november 2007
Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje Media:14BrM.jpg in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže.
Naloga
Mi bi radi na nekaj primerih pokazali, da z dodajanjem novih točk tem Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež.
Vzamemo torej eno od štirinajstih Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo:
1.) Ali je še Bravaisova mreža?
2.) Ali je nova Bravaisova mreža?
1. Primer:
Ortorombske Bravaisove mreže so štiri: simple, base-centered, body-centered in face centered. Zanima nas, če bi dobili novo Bravaisovo mrežo, če bi base-centered mreži dodali še dve točki tako, da bi bile štiri nasprotne ploskve ploskovno centrirane?