Bravaisove mreže
Iz Fizika trdne snovi 2007 - 2008
| Redakcija: 17:24, 23 november 2007 (spremeni) Bmikuz (Pogovor | prispevki) ← Pojdi na prejšnje urejanje |
Trenutna redakcija (01:54, 24 november 2007) (spremeni) (undo) Bmikuz (Pogovor | prispevki) |
||
| ( not shown.) | |||
| Vrstica 1: | Vrstica 1: | ||
| - | Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje [[Slika:14 Bravaisovih mrež.gif]] in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže. | + | Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje [[Media:14BrM.jpg]] in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže. |
| - | Mi bi radi na nekaj primerih pokazali, da z dodajanjem novih točk tem Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež. Vzamemo torej eno od 14 Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo: | + | |
| - | 1. Ali je še Bravaisova mreža? | + | =Naloga= |
| - | 2.Ali je nova Bravaisova mreža? | + | |
| + | Radi bi na nekaj primerih pokazali, da z dodajanjem novih točk obstoječim Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež. | ||
| + | |||
| + | Vzamemo torej eno od štirinajstih Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo: | ||
| + | |||
| + | 1.) Ali je še Bravaisova mreža? | ||
| + | |||
| + | 2.) Ali je nova Bravaisova mreža? | ||
| + | |||
| + | ==1. Primer:== | ||
| + | |||
| + | Ortorombske Bravaisove mreže so štiri: preprosta, s centrirano ploskvijo C, telesno centrirana in ploskovno centrirana. Zanima nas, če bi dobili novo Bravaisovo mrežo, če bi imeli mrežo s centrirano ploskvijo A in s centrirano ploskvijo B? | ||
| + | |||
| + | [[Slika:SLIKA1.jpg]] | ||
| + | |||
| + | Na skici sta narisani dve sosednji ortorombski celici, ki imata vsaka po dve nasprotni centrirani ploskvi. Če se premaknemo iz katerekoli točke B v smeri rdečega ali modrega vektorja pridemo do sosednje mrežne točke, medtem ko če isti premik opravimo iz katerekoli točke A naletimo na praznino. '''Ker okolica vsake točke ni popolnoma enaka, to ni BM!''' | ||
| + | |||
| + | ==2. Primer:== | ||
| + | |||
| + | Triklinski sistem ima samo preprosto Bravaisovo mrežo. Ali so telesno centrirana, ploskovno centrirana in mreža s ploskovno centrirano ploskvijo C nove BM v triklinskem sistemu? | ||
| + | |||
| + | [[Slika:SLIKA2.jpg]] [[Slika:SLIKA4.jpg]] | ||
| + | |||
| + | Prva skica prikazuje telesno centrirano triklinsko mrežo, druga skica pa ploskovno centrirano triklinsko mrežo. V obeh primerih se izkaže, da obstaja manjša osnovna celica (paralelpipeid), ki jo napenjajo trije rdeče označeni vektorji. Isto se da pokazati tudi za triklinsko mrežo s centrirano ploskvijo C. '''Ker se v navedenih mrežah vedno najde manjšo triklinsko preprosto BM, to niso nove BM!''' | ||
| + | |||
| + | ==3. Primer:== | ||
| + | |||
| + | Tetragonalni BM sta dve (preprosta in telesno centrirana). Zakaj ne obstajata tudi tetragonalna ploskovno centrirana BM in tetragonalna BM s centrirano ploskvijo C? | ||
| + | |||
| + | [[Slika:SLIKA5.jpg]] [[Slika:SLIKA6.jpg]] | ||
| + | |||
| + | Prva skica prikazuje tetragonalno mrežo s centrirano ploskvijo C. To ni nova BM, ker lahko v taki mreži vedno dobimo tetragonalno preprosto BM (modra barva) z manjšo prostornino. | ||
| + | |||
| + | Druga skica prikazuje tetragonalno ploskovno centrirano mrežo. To ni nova BM, ker lahko v taki mreži vedno dobimo tetragonalno telesno centrirano BM (modra barva) z manjšo prostornino. | ||
| + | |||
| + | ==4. Primer:== | ||
| + | |||
| + | Kubične BM so tri: preprosta, ploskovno centrirana in telesno centrirana. Ali je mreža s centrirano ploskvijo C nova BM v kubičnem sistemu? | ||
| + | |||
| + | [[Slika:SLIKA7.jpg]] | ||
| + | |||
| + | Ko smo preprosti kubični BM dodali dve točki na nasprotnih stranicah kocke, smo podrli rotacijsko simetrijo mreže. '''Ta mreža ni več kubična pač pa tetragonalna!''' | ||
Trenutna redakcija
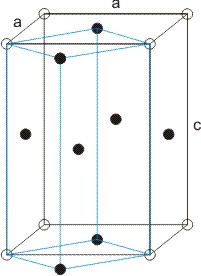
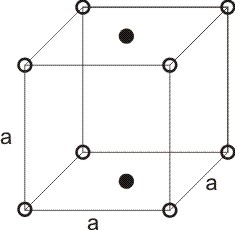
Bravais je leta 1848 pokazal, da iz simetrije kristala in točkovnih simetrijskih operacij (rotacija, zrcaljenje in inverzija) izhaja največ 14 različnih načinov, kako uredimo točke po prostoru, da bodo še translacijsko periodične. Povedano drugače imamo 7 kristalnih sistemov (triklinski, monoklinski, ortorombski, tetragonalni, kubični, heksagonalni in trigonalni) kot prikazuje Media:14BrM.jpg in nekateri od teh imajo več možnih mrež. Vseh možnih mrež je 14. To so Bravaisove mreže.
Vsebina |
[spremeni] Naloga
Radi bi na nekaj primerih pokazali, da z dodajanjem novih točk obstoječim Bravaisovim mrežam, ne moremo dobiti novih Bravaisovih mrež.
Vzamemo torej eno od štirinajstih Bravaisovih mrež, ji dodamo na poljubna mesta nove točke in se vprašamo:
1.) Ali je še Bravaisova mreža?
2.) Ali je nova Bravaisova mreža?
[spremeni] 1. Primer:
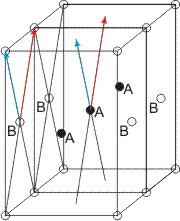
Ortorombske Bravaisove mreže so štiri: preprosta, s centrirano ploskvijo C, telesno centrirana in ploskovno centrirana. Zanima nas, če bi dobili novo Bravaisovo mrežo, če bi imeli mrežo s centrirano ploskvijo A in s centrirano ploskvijo B?
Na skici sta narisani dve sosednji ortorombski celici, ki imata vsaka po dve nasprotni centrirani ploskvi. Če se premaknemo iz katerekoli točke B v smeri rdečega ali modrega vektorja pridemo do sosednje mrežne točke, medtem ko če isti premik opravimo iz katerekoli točke A naletimo na praznino. Ker okolica vsake točke ni popolnoma enaka, to ni BM!
[spremeni] 2. Primer:
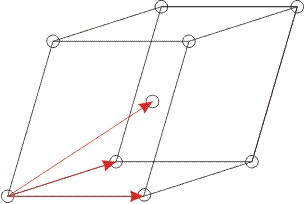
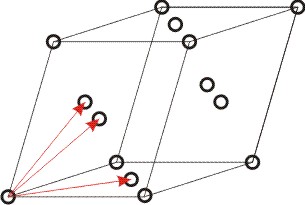
Triklinski sistem ima samo preprosto Bravaisovo mrežo. Ali so telesno centrirana, ploskovno centrirana in mreža s ploskovno centrirano ploskvijo C nove BM v triklinskem sistemu?
Prva skica prikazuje telesno centrirano triklinsko mrežo, druga skica pa ploskovno centrirano triklinsko mrežo. V obeh primerih se izkaže, da obstaja manjša osnovna celica (paralelpipeid), ki jo napenjajo trije rdeče označeni vektorji. Isto se da pokazati tudi za triklinsko mrežo s centrirano ploskvijo C. Ker se v navedenih mrežah vedno najde manjšo triklinsko preprosto BM, to niso nove BM!
[spremeni] 3. Primer:
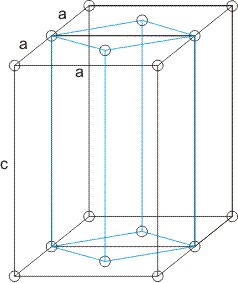
Tetragonalni BM sta dve (preprosta in telesno centrirana). Zakaj ne obstajata tudi tetragonalna ploskovno centrirana BM in tetragonalna BM s centrirano ploskvijo C?
Prva skica prikazuje tetragonalno mrežo s centrirano ploskvijo C. To ni nova BM, ker lahko v taki mreži vedno dobimo tetragonalno preprosto BM (modra barva) z manjšo prostornino.
Druga skica prikazuje tetragonalno ploskovno centrirano mrežo. To ni nova BM, ker lahko v taki mreži vedno dobimo tetragonalno telesno centrirano BM (modra barva) z manjšo prostornino.
[spremeni] 4. Primer:
Kubične BM so tri: preprosta, ploskovno centrirana in telesno centrirana. Ali je mreža s centrirano ploskvijo C nova BM v kubičnem sistemu?
Ko smo preprosti kubični BM dodali dve točki na nasprotnih stranicah kocke, smo podrli rotacijsko simetrijo mreže. Ta mreža ni več kubična pač pa tetragonalna!