Gostota stanj in stisljivost elektronskega plina

Iz Fizika trdne snovi 2007 - 2008

(Primerjava redakcij)

Skoči na: navigacija, iskanje

Redakcija: 07:43, 3 april 2008

Vsebina

1 Naloga
2 Gostota stanj
- 2.1 3D
- 2.2 2D
- 2.3 1D
3 Stisljivost
4 Povzetek

Naloga

Izračunaj gostoto stanj in stisljivost Fermijevega plina elektronov v treh, dveh in eni razsežnosti.

Gostota stanj

3D

Obravnavamo plin elektronov, zaprtih v kocko z robom L in prostornino V = L³. Gostota stanj g(ε) pove, koliko delcev v sistemu ima dano energijo ε:

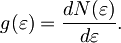
$g(\varepsilon)=\frac{dN(\varepsilon)}{d\varepsilon}.$

Stanja z dano energijo ε(k) v prostoru valovnih vektorjev k ležijo v krogelni lupini debeline dk s prostornino

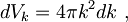
$dV_k = 4 \pi k^2 dk \ ,$

vsako stanje v njej pa zaseda

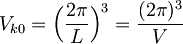
$V_{k0}=\Bigl(\frac{2 \pi}{L}\Bigr)^3 = \frac{(2\pi)^3}{V}$

prostora. V vsakem stanju se lahko nahajata dva elektrona z nasprotnim spinom, tako da za gostoto stanj dobimo

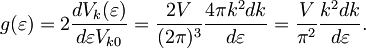
$g(\varepsilon) = 2 \frac{dV_k(\varepsilon)}{d\varepsilon V_{k0}} = \frac{2V}{(2\pi)^3} \frac{4 \pi k^2 dk}{d\varepsilon} = \frac{V}{\pi^2}\frac{k^2dk}{d\varepsilon}.$

Da jo izrazimo le z energijo, upoštevamo zvezo

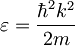
$\varepsilon = \frac{\hbar^2k^2}{2m}$

in njen odvod

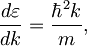
$\frac{d\varepsilon}{dk} = \frac{\hbar^2k}{m},$

pa dobimo končno obliko

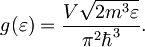
$g(\varepsilon) = \frac{V\sqrt{2m^3\varepsilon}}{\pi^2 \hbar^3} .$

Gostota stanj v treh razsežnostih z energijo korensko narašča.

2D

Tokrat so elektroni omejeni na površino S s stranicama L. Stanja z enako energijo sedaj ležijo na kolobarju s površino

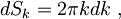
$dS_k = 2 \pi k dk \ ,$

od katere je vsakemu pripada

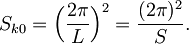
$S_{k0} = \Bigl(\frac{2\pi}{L}\Bigr)^2 = \frac{(2\pi)^2}{S}.$

Zveza med energijo in valovnim vektorjem je seveda za vse razsežnosti enaka, tako da za gostoto stanj dobimo

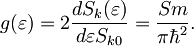
$g(\varepsilon) = 2 \frac{dS_k(\varepsilon)}{d\varepsilon S_{k0}} = \frac{Sm}{\pi\hbar^2}.$

V dveh dimenzijah torej ni odvisna od energije.

1D

Če se elektroni lahko gibljejo le po daljici dolžine L, namesto krogelne lupine oz. kolobarja stanj z določeno energijo ostaneta le še dva intervala

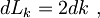
$dL_k = 2dk \ ,$

posamezno stanje pa zavzema

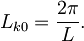
$L_{k0}=\frac{2\pi}{L}.$

Gostota stanj je v tem primeru enaka

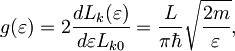
$g(\varepsilon) = 2 \frac{dL_k(\varepsilon)}{d\varepsilon L_{k0}} = \frac{L}{\pi\hbar} \sqrt{\frac{2m}{\varepsilon}},$

torej z naraščajčo energijo pada.

Stisljivost

Stisljivost opazovanega sistema je količina, ki pove, za koliko se mu zmanjša prostornina V, če malo povečamo tlak p, v primerjavi z začetno prostornino:

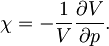
$\chi = -\frac{1}{V} \frac{\partial V}{\partial p}.$

V tem primeru bo prikladneje izračunati njeno obratno vrednost - modul stisljivosti K

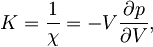
$K = \frac{1}{\chi} = -V \frac{\partial p}{\partial V},$

saj bomo tlak dobili iz definicije

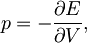
$p = - \frac{\partial E}{\partial V},$

torej iz povečanja energije sistema E ob zmanjšaju njegove prostornine. Energijo izračunamo tako, da seštejemo prispevke vseh delcev. Ti pri temperaturi T = 0 zasedajo stanja do Fermijeve energije ε_F:

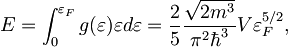
$E = \int_0^{\varepsilon_F} g(\varepsilon) \varepsilon d\varepsilon = \frac{2}{5} \frac{\sqrt{2m^3}}{\pi^2\hbar^3} V\varepsilon_F^{5/2},$

kjer pa je tudi Fermijeva energija odvisna od prostornine. V k prostoru N delcev zaseda stanja do k_F, ki ustreza ε_F:

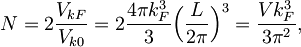
$N = 2 \frac{V_{kF}}{V_{k0}} = 2 \frac{4\pi k_F^3}{3} \Bigl(\frac{L}{2\pi}\Bigr)^3 = \frac{V k_F^3}{3\pi^2},$

od koder lahko izrazimo Fermijev valovni vektor in ga nadomestimo s Fermijevo energijo

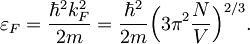
$\varepsilon_F = \frac{\hbar^2 k_F^2}{2m}= \frac{\hbar^2}{2m} \Bigl(3\pi^2 \frac{N}{V}\Bigr)^{2/3}.$

Ko dobljeno vstavimo nazaj v izraz za celotno energijo, ostane

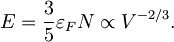
$E = \frac{3}{5}\varepsilon_F N \propto V^{-2/3}.$

Tlak sedaj dobimo z odvajanjem energije

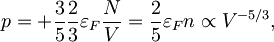
$p = + \frac{3}{5}\frac{2}{3}\varepsilon_F\frac{N}{V} = \frac{2}{5} \varepsilon_F n \propto V^{-5/3},$

kjer je n številska gostota delcev. Stisljivostni modul sledi s še enim odvodom

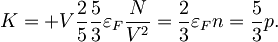
$K = + V \frac{2}{5}\frac{5}{3}\varepsilon_F\frac{N}{V^2} = \frac{2}{3} \varepsilon_F n = \frac{5}{3}p.$

V dveh oz. eni razsežnosti je ob upoštevanju drugačne gostote stanj in smiselno spremenjenih definicijah tlaka in stisljivosti postopek povsem enak. Rezultati so zbrani v spodnji preglednici.

Povzetek

	3D	2D	1D
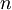
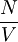
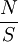
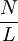
$n \$	$\frac{N}{V}$	$\frac{N}{S}$	$\frac{N}{L}$
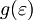
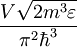
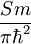
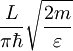
$g(\varepsilon)$	$\frac{V\sqrt{2m^3\varepsilon}}{\pi^2 \hbar^3}$	$\frac{Sm}{\pi\hbar^2}$	$\frac{L}{\pi\hbar} \sqrt{\frac{2m}{\varepsilon}}$
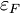
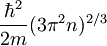
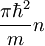
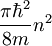
$\varepsilon_F$	$\frac{\hbar^2}{2m} (3\pi^2 n)^{2/3}$	$\frac{\pi\hbar^2}{m} n$	$\frac{\pi\hbar^2}{8m} n^2$
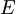
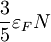
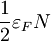
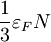
$E \$	$\frac{3}{5} \varepsilon_F N$	$\frac{1}{2} \varepsilon_F N$	$\frac{1}{3} \varepsilon_F N$
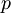
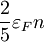
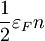
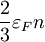
$p \$	$\frac{2}{5} \varepsilon_F n$	$\frac{1}{2} \varepsilon_F n$	$\frac{2}{3} \varepsilon_F n$
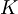
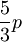
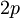
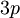
$K \$	$\frac{5}{3} p$	$2p \$	$3p \$

Vzpostavljeno iz »http://burana.ijs.si/wiki3/index.php/Gostota_stanj_in_stisljivost_elektronskega_plina«

 <math>
-dV_k = 4 \pi k^2 dk,
+dV_k = 4 \pi k^2 dk \ ,
 </math>
 <math>
-dS_k = 2 \pi k dk,
+dS_k = 2 \pi k dk \ ,
 </math>
 <math>
-dL_k = 2dk,
+dL_k = 2dk \ ,
 </math>
 !width="150"| 1D
 |-style="height:60px"
-! <math> n </math>
+! <math> n \  </math>
 | <math> \frac{N}{V} </math>
 | <math> \frac{N}{S} </math>
 | <math> \frac{\pi\hbar^2}{8m} n^2 </math>
 |-style="height:60px"
-! <math> E </math>
+! <math> E \  </math>
 | <math> \frac{3}{5} \varepsilon_F N </math>
 | <math> \frac{1}{2} \varepsilon_F N </math>
 | <math> \frac{1}{3} \varepsilon_F N </math>
 |-style="height:60px"
-! <math> p </math>
+! <math> p \ </math>
 | <math> \frac{2}{5} \varepsilon_F n </math>
 | <math> \frac{1}{2} \varepsilon_F n </math>
 | <math> \frac{2}{3} \varepsilon_F n </math>
 |-style="height:60px"
-! <math> K </math>
+! <math> K \ </math>
 | <math> \frac{5}{3} p </math>
-| <math> 2p </math>
+| <math> 2p \ </math>
-| <math> 3p </math>
+| <math> 3p \ </math>
 |}