Harmonski oscilator II

(Primerjava redakcij)

Current revision as of 11:59, 25. marec 2010

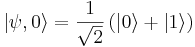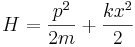Kako se s časom spreminjajo pričakovane vrednosti operatorjev $x$ , $x 2$ , $p$ , $H$ in $H 2$ v stanju $\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)$ harmonskega oscilatorja $H=\frac{p^2}{2m}+\frac{kx^2}{2}$ ?
Preveri veljavnost Ehrenfestovega teorema za položaj delca in nejgovo gibalno količino.
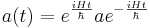Izračunaj časovno odvisnost anihilacijskega operatorja $a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}$ in rezultat uporabi za izračun količin iz naloge 1.

@@ Vrstica 1: / Vrstica 1: @@
-# Kako se s časom spreminjajo pričakovane vrednosti operatorjev <math>x</math>, <math>x^2</math>, <math>p</math>, <math>H</math> in <math>H^2</math>v stanju <math>\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)</math> harmonskega oscilatorja <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>?
+# Kako se s časom spreminjajo pričakovane vrednosti operatorjev <math>x</math>, <math>x^2</math>, <math>p</math>, <math>H</math> in <math>H^2</math> v stanju <math>\left|\psi,0\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)</math> harmonskega oscilatorja <math>H=\frac{p^2}{2m}+\frac{kx^2}{2}</math>?
 # Preveri veljavnost Ehrenfestovega teorema za položaj delca in nejgovo gibalno količino.
 # Izračunaj časovno odvisnost anihilacijskega operatorja <math>a(t)=e^{\frac{iHt}{\hbar}}ae^{-\frac{iHt}{\hbar}}</math> in rezultat uporabi za izračun količin iz naloge 1.