Harmonski oscilator II

Iz Kvantna Mehanika I 2006 - 2007

Naloga

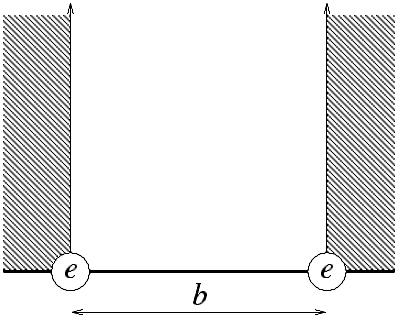
Potencial, ki ga čuti elektron, lahko opišemo z neskončno potencialno jamo s širino b, na robovih katere sta pritrjena delca z nabojem e (glej skico). Če je naboj e negativen in je širina potencialne jame dovolj velika, je potencial, ki ga elektron čuti v v nizkoenergijskih stanjih sistema v prvem približku harmonski.

1. Določi lastne energije elektrona v približku harmonskega potenciala.
2. Če je širina potencialne jame premajhna, postane pomemben tudi anharmonski del potenciala. Oceni, najmanj kolikšen mora biti b, da je harmonski približek upravičen za osnovno stanje sistema. Harmonski približek je veljaven, če je pričakovana vrednost anharmonskega dela potenciala v osnovnem stanju sistema bistveno manjša od razmika med energijskimi nivoji. Upoštevaj, da je pri majhnih odstopanjih od harmonskega potenciala pomemben samo najnižji neharmonski člen v razvoju potenciala v Taylorjevo vrsto.
3. Elektron je v osnovnem stanju sistema. Ob t = 0 v trenutku spremenimo naboja na robovih potencialne jame za faktor α² (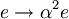). S kolikšno verjetnostjo najdemo elektron v osnovnem stanju novega sistema?
4. Določi verjetnost, da je po spremembi elektron v n-tem vzbujenem stanju novega sistema. Namig: Izrazi stari anihilacijski operator kot linearno kombinacijo novega anhilacijskega in kreacijskega operatorja ter poišči rekurzijsko povezavo med koeficienti v razvoju začetne valovne funkcije po lastnih stanjih novega potenciala.

Rešitev